Question

Найдите уравнение касательной к кривой y=3x-4/2x-3, параллельных прямой y=-x+3

Answer 1

уравнения касательных у₁ = -х + 2;  у₂ = -х + 4

Пошаговое объяснение:

Прежде всего найдем уравнение касательной.

Уравнение касательной имеет вид

$y_k = y_0 + y'(x_0)(x - x_0)$

$\displaystyle y'=\bigg(\frac{3x-4}{2x-3}\bigg) '=\bigg[\;\bigg(\frac{u}{v} \bigg)'=\frac{u'v-v'u}{v^2}\;\bigg] =$

$\displaystyle =\frac{(3x-4)'*(2x-3)-(3x-4)*(2x-3)'}{(2x-3)^2} =\frac{6x-9-(6x-8)}{(2x-3)^2} =\frac{-1}{(2x-3)^2}$

Рассмотрим уравнение касательной  в точке х₀ (эту точку нам и надо найти)

$\displaystyle y_k = y_0 + y'(x_0)(x - x_0)y_k = y_0 + \bigg(\frac{-1}{(2x-3)^2}\bigg)(x - x_0)$

Для того, чтобы две прямые были параллельны, необходимо,  чтобы в уравнениях прямых коэффициенты при х были бы равны.

У прямой у = -x + 3  коэффициент при х равен -1

У касательной коэффициент при х равен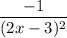   $\displaystyle \frac{-1}{(2x-3)^2}$

Приравняем коэффициенты и найдем х₀

$\displaystyle \frac{-1}{(2x-3)^2} =-1(2x-3)^2 = 1;\quad (2x-3)=\pm12x-3 = 1;\quad \boldsymbol {x= 2};2x-3 = -1;\quad \boldsymbol {x= 1};$

Таким образом, у нас есть две точки касания, в которых касательная будет параллельна прямой у = -х +3

Найдем уравнение касательной в точке  х₀ = 1

Подставим  х₀ в формулу касательной.

$\displaystyle y'( 1) = -\frac{1}{(2*1-3)^2} =-1y(1) = \frac{3*1-4}{2*1-3} =\frac{-1}{-1} =1y_k=1-1(x-1)boldsymbol{y_k= -x+2}$    - это уравнение касательной в точке х₀= 1.

И эта прямая ║ прямой у = -x +3

Найдем уравнение касательной в точке  х₀ = 2

Подставим  х₀ в формулу касательной.

$\displaystyle y'( 2) = -\frac{1}{(2*2-3)^2} =-1y(2) = \frac{3*2-4}{2*2-3} =\frac{2}{1} =2y_k=2-1(x-2)boldsymbol{y_k= -x+4}$- это уравнение касательной в точке х₀= 2.

И эта прямая ║ прямой у = -x +3

Таким образом, кривая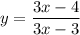    $\displaystyle y=\frac{3x-4}{3x-3}$   имеет две касательных, параллельных прямой y= -x + 3