ответ:Биссектриса делит угол, из которого выходит, пополам. От сюда, можно узнать что углы ∠ABD и ∠DBC=80/2=40°
Рассмотрим треугольник ABD, в нем мы знаем два угла: ADB и ABD. Зная два угла в треугольнике можно найти третий угол, т. к. сумма углов в треугольнике равна 180°. Тогда: 180°-(40°+120°)=20°. Т. е. угол ∠DAB = 20°;
Теперь рассмотрим треугольник ABC, в нем мы теперь знаем два угла: ∠A (равен углу ∠DAB ) и угол ∠B, отсюда можно найти третий угол ∠C: 180°-(20°+80°)=80°.
Рассмотри треугольник DBC, в нем нам известны два угла ∠DBC и ∠C, найдем третий угол: 180°-(40°+80°)=60°.
ответ: В треугольнике CBD углы: ∠CBD=40°, ∠C=80°, ∠CDB=60°.
В решении.
Пошаговое объяснение:
1. Даны множества А = {1, 2, 3, 4, 5, 6, 7} и В = {4, 6, 8}. Перечислите элементы, образующие множество С=А∩В. Изобразите множества А, В и С графически.
А = {1, 2, 3, 4, 5, 6, 7}
В = {4, 6, 8}
С=А∩В = {4, 6}
Множество С - это множество, образованное пересечением множеств А и В, то есть, в него входят элементы, входящие в оба множества.
Графически: с кругов Эйлера:
один круг частично перекрывает второй круг, общая часть двух кругов в виде небольшого эллипса (элементов всего два) и является множеством С.
Остальная часть первого круга - множество А, остальная часть второго круга - множество В.
2. Даны множества А = {1, 2, 3, 4, 5, 6, 7} и В = {4, 6, 8}. Перечислите элементы, образующие множество С= А\В. Изобразите множества А, В и С графически.
А = {1, 2, 3, 4, 5, 6, 7}
В = {4, 6, 8}
С= А\В = {1, 2, 3, 5, 7}
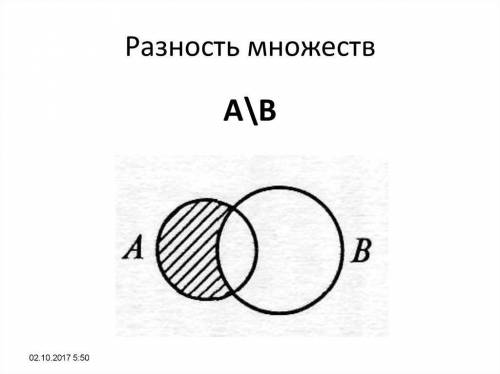
Множество С - это множество является разностью между множествами А и В и включает только элементы множества А, не принадлежащие множеству В.
Графически: с кругов Эйлера.
Закрашенная часть на рисунке - множество С.
Первый круг полностью - множество А, второй - множество В.
Б) 10
Пошаговое объяснение:
СD=m медиана
2m=√(2AC²+2BC²-AB²)
AB=2m AC=16 BC=12
4m²=2*(16²+12²)-4m²
8m²=16²+12²
m²=100
m=10