а) Найдем точки, в которых модули превращаются в ноль: ; , и , .
Разобьем числовую прямую этими точками на четыре промежутка. На каждом из этих промежутков знак каждого из подмодульных выражений постоянен, что позволяет нам раскрыть модули по определению:
I.
Так как , найденное значение является корнем уравнения.
II.
Так как , то на данном промежутке уравнение корней не имеет.
III.
Получили тождественно верное равенство, значит все числа из промежутка являются корнями данного уравнения.
IV.
Так как , то значение является корнем данного уравнения.
Собирая найденные ответы, получаем:
б) Модули превращаются в ноль в точках
и
которые разбивают числовую прямую на четыре промежутка.
I.
Так как найденное число является корнем уравнения.
II.
Так как в результате получили ложное равенство, на данном промежутке уравнение не имеет корней.
III.
Так как на данном промежутке уравнение не имеет корней.
IV.
Так как то найденное число является корнем уравнения.
Собирая найденные ответы, получаем:
в) Так как , достаточно рассмотреть два промежутка, на которые числовую прямую разбивает точка .
I.
На данном промежутке уравнение не имеет корней
II.
Оба числа больше , поэтому являются корнями данного уравнения.
Семейные традиции — это обычные принятые в семье нормы, манеры поведения, обычаи и взгляды, которые передаются из поколения в поколение. Семейные традиции и ритуалы являются, с одной стороны, одним из важных признаков здоровой (по определению В.Сатир) или функциональной (по определению Э. Г. Эйдемиллера и других исследователей) семьи, а, с другой стороны, наличие семейных традиций является одним из важнейших механизмов передачи следующим поколениям семьи законов внутри семейного взаимодействия: распределения ролей во всех сферах семейной жизни, правил внутри семейного общения, в том числе разрешения конфликтов и преодоления возникающих проблем.
а)![x \in \{ - 4\} \cup [ - 1;\,\,0];](/tpl/images/4978/9297/847f0.png)
б)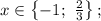
в)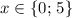
Пошаговое объяснение:
а) Найдем точки, в которых модули превращаются в ноль: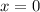 ;
; 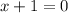 ,
, 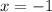 и
и 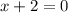 ,
,  .
.
Разобьем числовую прямую этими точками на четыре промежутка. На каждом из этих промежутков знак каждого из подмодульных выражений постоянен, что позволяет нам раскрыть модули по определению:
I.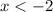
Так как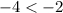 , найденное значение является корнем уравнения.
, найденное значение является корнем уравнения.
II.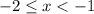
Так как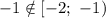 , то на данном промежутке уравнение корней не имеет.
, то на данном промежутке уравнение корней не имеет.
III.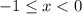
Получили тождественно верное равенство, значит все числа из промежутка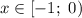 являются корнями данного уравнения.
являются корнями данного уравнения.
IV.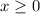
Так как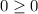 , то значение
, то значение 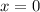 является корнем данного уравнения.
является корнем данного уравнения.
Собирая найденные ответы, получаем:
б) Модули превращаются в ноль в точках
которые разбивают числовую прямую на четыре промежутка.
I.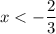
Так как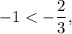 найденное число является корнем уравнения.
найденное число является корнем уравнения.
II.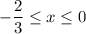
Так как в результате получили ложное равенство, на данном промежутке уравнение не имеет корней.
III.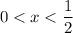
Так как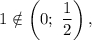 на данном промежутке уравнение не имеет корней.
на данном промежутке уравнение не имеет корней.
IV.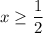
Так как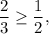 то найденное число является корнем уравнения.
то найденное число является корнем уравнения.
Собирая найденные ответы, получаем:
в) Так как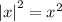 , достаточно рассмотреть два промежутка, на которые числовую прямую разбивает точка
, достаточно рассмотреть два промежутка, на которые числовую прямую разбивает точка 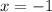 .
.
I.
На данном промежутке уравнение не имеет корней
II.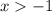
Оба числа больше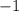 , поэтому являются корнями данного уравнения.
, поэтому являются корнями данного уравнения.