нет
Пошаговое объяснение:
Предположим, что такое разбиение возможно и оно выполнено. Обозначим меньшие числа в парах буквами a с индексами:
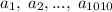
Индекс совпадает с разностью чисел в паре, в которой состоит соответствующее число.
Тогда большее число в 
-той паре будет равно 
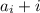, а их (бОльших чисел) последовательность выглядеть так:
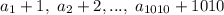
Вычислим сумму чисел от 1 до 2020 двумя . С одной стороны, ее можно найти как сумму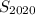 
первых 2020 элементов арифметической прогрессии с первым элементом 
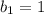и разностью 
:
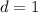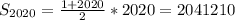
С другой стороны, можно сложить суммы в парах чисел, используя введенные буквенные обозначения:
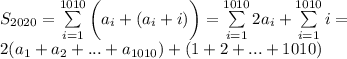
Сумму чисел во вторых скобках опять же найдем как сумму 
первых 1010 элементов арифметической прогрессии с первым элементом 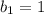и разностью :
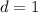Мы подошли к ключевому равенству: приравняем полученные разными путями суммы:
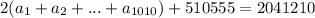
Отсюда
Однако сумма натуральных чисел не может быть дробной! Получили противоречие. А значит, разбиение, о котором идет речь в задаче, невозможно.
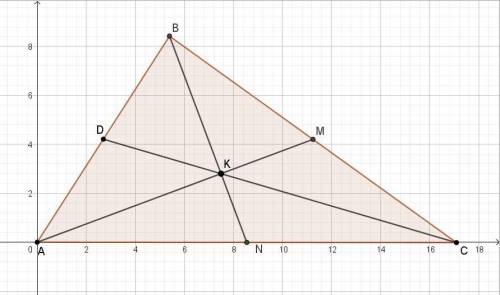
Надо воспользоваться свойством медиан треугольника:
сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон.
Если отрезок СК медианы равен 10, то сама медиана равна 15.
Примем отрезок КМ = х, тогда медиана АМ = 3х.
На основе условия задания, что медианы АМ и BN перпендикулярны, найдём длины сторон.
АВ² = 4х² + 36,
ВС² = 4(36 + х²),
АС² = 4(4х² + 9).
Применим свойство:
(3х)² + 9² + 15² = (3/4)( 4х² + 36 + 4(36 + х²) + 4(4х² + 9)).
Получаем 9х² = 144 или х² = 16, отсюда х = 4.
ответ: медиана АМ = 3*4 = 12.
Пошаговое объяснение:
Оцінити зверху ймовірність того, що при n підкиданнях грального кубика цифра 4 випаде
не менше, ніж m раз.
Розв 'язати для конкретних значень n m:
n =990 ,
m = 210
Ймовірність випадіння цифри 4 при одному підкиданні грального кубика дорівнює 1/6. Отже, ймовірність того, що цифра 4 НЕ випаде при одному підкиданні, дорівнює 5/6.
Для того, щоб знайти ймовірність того, що цифра 4 випаде не менше, ніж m раз, ми можемо скористатися біноміальним розподілом. Формула для біноміального розподілу має вигляд:
P(X>=m) = 1 - P(X<m) = 1 - C(n,m)(1/6)^m(5/6)^(n-m)
де X - кількість разів, коли цифра 4 випадає при n підкиданнях, С(n,m) - кількість ів вибрати m із n підкидань.
Підставляючи значення n=990 і m=210 в формулу, ми отримуємо:
P(X>=210) = 1 - P(X<210) = 1 - C(990,210)(1/6)^210(5/6)^(780)
де C(990,210) = 990! / (210! * (990-210)!) є кількістю ів вибрати 210 підкидань з 990.
Цю велику чисельну величину можна обчислити за до комп'ютера або калькулятора.
Отримуємо:
P(X>=210) ≈ 0.003
Таким чином, ймовірність того, що цифра 4 випаде не менше, ніж 210 раз при 990 підкиданнях грального кубика, дуже мала - близько 0.3%.