Question

Імовірність виготовлення на автоматичному верстаті стандартної деталі дорівнює 0,8. Скласти ряд розподілу числа стандартних деталей серед 4-х, узятих навмання деталей із числа виготовлених на цьому верстаті

Answer 1

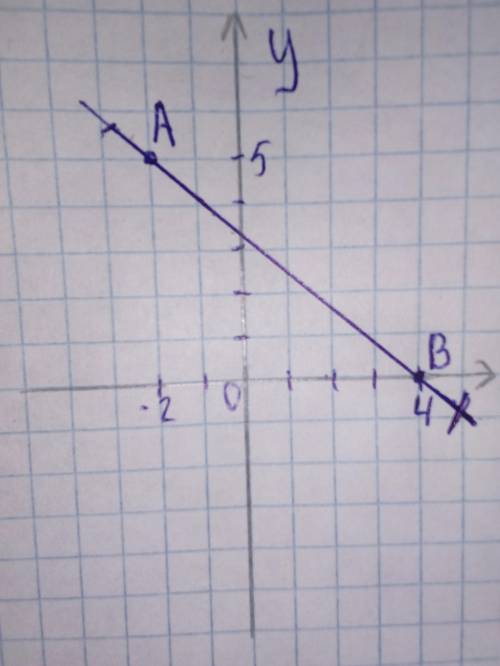
Відповідь:

Покрокове пояснення:

Щоб скласти ряд розподілу числа стандартних деталей серед 4-х, узятих навмання деталей із числа виготовлених на цьому верстаті, ми можемо використати біноміальний розподіл.

Біноміальний розподіл використовується для моделювання кількості успіхів у послідовності незалежних випробувань, де кожне випробування має два можливих результати: успіх або невдача.

У даному випадку, успіхом є виготовлення стандартної деталі на автоматичному верстаті з ймовірністю 0,8, а невдачею - невиготовлення з ймовірністю 1 - 0,8 = 0,2.

Ряд розподілу для 4-х деталей можна записати таким чином:

P(X = k) = C(n, k) * p^k * (1 - p)^(n - k),

де:

- P(X = k) - ймовірність отримати k успіхів (стандартних деталей),

- n - кількість випробувань (кількість деталей, узятих навмання),

- k - кількість успіхів (стандартних деталей),

- p - ймовірність успіху (ймовірність виготовлення стандартної деталі).

У нашому випадку, n = 4 (4 деталі), p = 0,8 (ймовірність виготовлення стандартної деталі).

Ряд розподілу для 4-х деталей буде виглядати так:

P(X = 0) = C(4, 0) * 0.8^0 * (1 - 0.8)^(4 - 0)

P(X = 1) = C(4, 1) * 0.8^1 * (1 - 0.8)^(4 - 1)

P(X = 2) = C(4, 2) * 0.8^2 * (1 - 0.8)^(4 - 2)

P(X = 3) = C(4, 3) * 0.8^3 * (1 - 0.8)^(4 - 3)

P(X = 4) = C(4, 4) * 0.8^4 * (1 - 0.8)^(4 - 4)

Де C(n, k) - біноміальний

коефіцієнт, який розраховується за формулою:

C(n, k) = n! / (k! * (n - k)!)

Застосувавши ці формули, ми можемо розрахувати ймовірності для кожного значення k від 0 до 4.