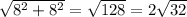, а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна 
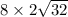, а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна 
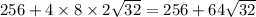Будем надеяться, что я не ошибся в вычислениях.
ответ: 1) 4 2) -49/600 3) - 0,7316/√9516
Пошаговое объяснение: 1) 1+tg²α= 1/Cos²α = 1/(-0,5)²= 1/0,25=4 2) Cosα = -0,96, ⇒ Sin²α= 1 - Cos²α= 1- (-0,96)²= 1 - (-24/25)²= 1 - 576/625 = 49/625, ⇒ Sinα·tgα =Sinα · Sinα/Cosα = Sin²α/Cosα= 49/625 : (-24/25) = - 49/600 3) Sinα=0,22 ⇒Cos²α = 1 - Sin²α = 1- (0,22)² = 1 - 0,0484=0,9516 ; 90°<α<180° , т.е. α∈2 четверти, поэтому Cosα<0 ⇒Cosα= - √0,9516; Cosα-tgα = Cosα - Sinα/Cosα = (Cos²α - Sinα) / Cosα = (0,9516 - 0,22)/(- √0,9516)= 0,7316/(-√9516)