Не знаю, чи буде зрозуміло словами, тому потім розпишу конкретно в цифрах.
В кінці залишається 1 яблуко. 3й хлопець отримує половину +3, звідси оці +3 та 1 яблуко - це половина нового залишку. Тобто у третього хлопця 4+3=7 яблук та +1 залишку - отримуємо 8 яблук, які залишись після другого хлопця.
Другий хлопець отримує половину +2. Такаж логіка, 8+2=10 - одна половина + друга половина, яку отримує цей хлопець. Тобто другий хлопець отримує 10+2=12 яблук (+8 нового залишку), то отримуємо 20 яблук, які залишились після першого хлопця.
Перший хлопець отримує половину +1. Половина цього залишку 20+1. Тоді перший хлопець отримав 21+1 яблуко.
21 яблуко - половина всіх яблук. Отже їх було 42.
А тепер схематично:
Всього 42 яблука.
1 хлопець = 42:2 +1= 21+1=22 яблука.
Залишається 42-22=20 яблук.
2 хлопець = 20:2+2=10+2=12 яблук
Залишається 20-12=8 яблук
3 хлопець = 8:2+3 = 4+3 = 7 яблук
Залишається 1 яблуко.
д)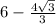 
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
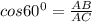
AB=AC·cosn60°=10·1/2=5,
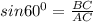
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
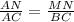или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
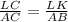или LC=AC·LK/AB=10·2/5=4.
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
д)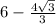
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
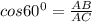
AB=AC·cosn60°=10·1/2=5,
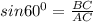
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
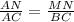или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
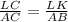или LC=AC·LK/AB=10·2/5=4.
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
Пошаговое объяснение:
Складаємо рівняння
Було Х яблук.
Х-3 - (х-3):3 -3= 1/2х
Х-3- 1/3х+1- 3= 1/2х
2/3х-6+1=1/2х
2/3х-5=1/2х
2/3х-1/2х=5
4/6х-3/6х=5
1/6х=5
Х=5:1/6
Х=5•6/1
Х=30
Відповідь: в кошику було 30 яблук
Перевірка
Х-3 - (х-3):3 -3= 1/2х
30-3-(30-3):3-3=1/2•30
27-27:3-3=30/2
27-9-3=15
15=15
Без рівняння перевірка
Було 30 яблук
30-3=27ябл залишилось коли забрали 3 яблука
27:3=9ябл 1/3 залишку
27-9=18 ябл залишилось
18-3=15ябл коли забрали ще 3 яблука
15ябл це 1/2 яблук що залишилось
30:2=15яблук половина всіх
Можна з кінця задачі
Х- всього яблук
Залишилось 1/2 Х
До того назад 3яблука повертаємо; це дві частини з трьох яблук залишку
1/2Х+3 це (1-1/3=2/3)
Весь залишок був
(1/2х+3):2•3= (1/2х+3)•1/2•3=
(1/2х+3)•3/2=
3/4х+9/2;
Ще 3 яблука до цього взяли
3+3/4х+9/2= 3+3/4х+4 1/2=
7 1/2+3/4х;
І це всі яблука були Х;
Х= 7 1/2+3/4х
Х-3/4х=7 1/2
1/4х= (7•2+1)/2
1/4х=15/2
Х=15/2:1/4
Х=15/2•4/1
Х=15/1•2/1
Х=30 яблук