все решала сама)
если ты дашь много , буду довольна.
астанадағы ұлттық мұражай-орталық азиядағы ең үлкен мұражай. палеолиттен бүгінгі күнге дейін – түрлі дәуірдегі экспонаттардың бай коллекциясы жалпы ауданы 74 мың шаршы метр жеті залға орналастырылды. мұражай жаңа демонстрациялық технологиялармен
жабдықталған.
1998 жылдың наурыз айында президент нұрсұлтан назарбаев халық бірлігі жылын өткізуге дайындық жөніндегі отырыста астанада қазақстанның ұлттық музейін құруды ұсынды. жобаны іске асыру бойынша дайындық жұмыстары басталды, он алты жыл өткен соң ол алғашқы келушілерді қабылдады.
ұлттық мұражай 2014 жылдың 2 шілдесінде президенттің қатысуымен салтанатты түрде ашылды.астанадағы ұлттық музейдің коллекциясы әр дәуірдің экспонаттарын қамтиды. экспозиция әлемдік стандарттардың талаптарына жауап беретін заманауи жабдықтары бар жеті залда орналасқан.
перевод:
национальный музей в астане – самый большой музей в центральной азии. богатейшая коллекция экспонатов разных эпох – от палеолита до наших дней - разместилась в семи залах общей площадью в 74 тыс. кв. метров. музей оснащен новейшими демонстрационными технологиями.
в марте 1998 года
президент нурсултан назарбаев на заседании по подготовке проведения года народного единства предложил создать в астане национальный музей казахстана. сразу же начались подготовительные работы по реализации проекта, и спустя шестнадцать лет он принял первых посетителей. национальный музей был
торжественно открыт в присутствии президента 2 июля 2014 года.коллекция национального музея в астане включает в себя экспонаты разных эпох. экспозиция расположена в семи залах с современным оборудованием, отвечающим требованиям мировых стандартов.
прости, что так много, выбери самое
главное.
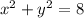 — уравнение окружности с центром
— уравнение окружности с центром 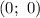 и радиусом
и радиусом 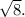
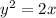 — уравнение параболы
— уравнение параболы
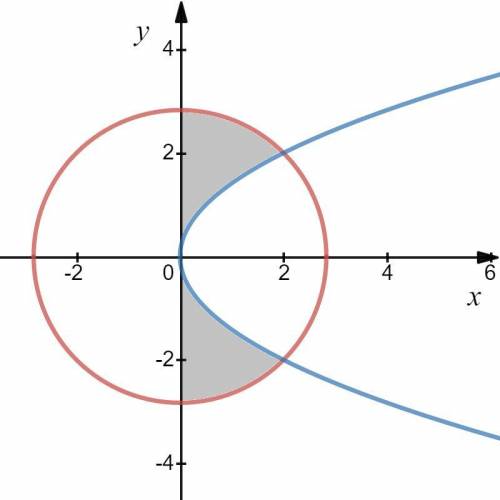
Изобразим графики данных уравнений и найдем площадь образовавшейся фигуры в правой полуплоскости.
Выразим ординаты данных уравнений:
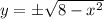 и
и 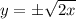
Так как имеем симметричные фигуры, найдем площадь 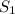 одной из них. Общая их площадь
одной из них. Общая их площадь 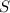 будет состоять из площади двух
будет состоять из площади двух 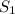 , то есть
, то есть 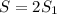
Тогда 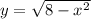 и
и 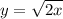 . Поэтому
. Поэтому 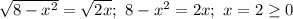
Так как окружность вытесняет больше площади, чем парабола, то имеем разность их площадей, определяющаяся через определенный интеграл:
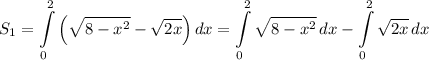
Найдем первый интеграл геометрически: площадь круга находится по формуле 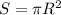 , где
, где 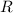 — радиус круга. Тогда четверть круга:
— радиус круга. Тогда четверть круга: 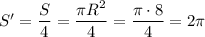
Найдем второй интеграл по формуле Ньютона-Лейбница:
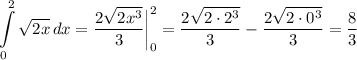
Таким образом, 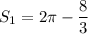 кв. ед.
кв. ед.
Тогда 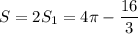 кв. ед.
кв. ед.
ответ: 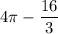 кв. ед.
кв. ед.
1)б
2)г
3)б
4)в
5)г
6)я не знаю