Question

Обчисліть площу плоскої фігури, обмеженої лініями y=-1/x y=x^2 y=x^2/8

Answer 1

Пошаговое объяснение:

Фигура ограничена линиями $$y=-1/x$, $y=x^2$ и $y=x^2/8$$.

Точки пересечения графиков можно найти, решив систему уравнений:

$\begin{cases}$

$y = -\frac{1}{x}$

$y = x^2$

$y = \frac{x^2}{8}$

$\end{cases}$

Первые два уравнения можно решить методом подстановки:

$$$$

$-\frac{1}{x} = x^2 \Rightarrow x^3 = -1 \Rightarrow x = -1$$$

Тогда $y = -1/(-1) = 1$, и точка пересечения первых двух графиков имеет координаты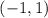 $$(-1, 1)$$

1 = $\frac{x^2}{8} \Rightarrow x = \pm 2\sqrt{2}$$$

Таким образом, точки пересечения всех трех графиков имеют координаты $$(-1, 1)$ и $(2\sqrt{2}, 2)$$

Площадь фигуры можно найти, разбив ее на две части: треугольник и фигуру, ограниченную кривыми $$y=x^2$ и $y=x^2/8$$

Площадь треугольника равна:

S_${\text{треугольника}} = \frac{1}{2} \cdot 2\sqrt{2} \cdot (2 - 1) = \sqrt{2}$$$

Площадь фигуры между кривыми $y=x^2$ и $y=x^2/8$ можно найти, вычислив интеграл:

S_${\text{фигуры}} = \int_{-\sqrt{2}}^{\sqrt{2}} \left(x^2 - \frac{x^2}{8}\right) dx = \frac{15}{8} \sqrt{2}$$$

Таким образом, общая площадь фигуры равна:

S = S$_{\text{треугольника}} + S_{\text{фигуры}} = \sqrt{2} + \frac{15}{8} \sqrt{2} = \frac{23}{8} \sqrt{2}$$$

ответ: $$\frac{23}{8} \sqrt{2}$$