1. Измерение отрезков
Две геометрические фигуры (отрезки, углы,
треугольники и др.) считаются равными, если их
можно наложить друг на друга так, чтобы они совпали.
Отрезки равны, если равны их длины.
Если точка лежит на отрезке , то A B C
+ = .
1. На прямой выбраны три точки , и , причём = 3, = 5. Чему может быть равно ?
(Есть разные возможности.)
B Если точка находится между точками и
A B C
3 5
, то это расстояние равно 3+5 = 8. Но возможен и
другой случай, когда находится вне отрезка .
Нарисовав картинку, убеждаемся, что в этом случае
B A C расстояние равно 5 − 3 = 2. C
3 2
2. На прямой выбраны четыре точки , , ,
, причём = 1, = 2, = 4. Чему может
быть равно ? Укажите все возможности.
B Сначала посмотрим, чему может быть равно
расстояние между точками и . Как и в предыдущей задаче, тут есть две возможности (точка
внутри или вне) | и получается либо 3, либо
1. Теперь мы получаем две задачи: в одной из них
= 3 и = 4, в другой | = 1, = 4.
Каждая имеет по два ответа, так что всего ответов
получается четыре: 4+3, 4−3, 4+1 и 4−1. ответ:
расстояние может равняться 1, 3, 5 или 7. C
3. На деревянной линейке отмечены три деле- 0 7 11
ния: 0, 7 и 11 сантиметров. Как отложить с её отрезок в (а) 8 см; (б) 5 см?
B Используя деления 7 и 11, легко отложить 4
сантиметра. Сделав это дважды, получим отрезок
в 8 сантиметров. Отложить 5 сантиметров немного
сложнее: умея откладывать 8 и 7, можно отложить
1 сантиметр. Сделав это 5 раз, получаем 5 сантиметров. C
6
Можно сделать иначе: мы умеем откладывать
4 см и 1 см, так что можно отложить их подряд
и получить 5 cм. Ещё один так что достаточно отложить 3 раза по 11 см и потом 4 раза по 7 в другую сторону. (Преимущество
приведённого сначала в том, что он годится
для любого целого числа сантиметров.)
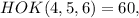
 где
где  – некоторое целое число.
– некоторое целое число.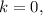 тогда
тогда 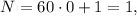 но
но  не делится на
не делится на  а значит не подходит.
а значит не подходит.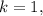 тогда
тогда 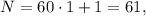 но
но 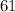 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 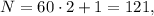 но
но 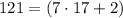 не делится на
не делится на  а значит не подходит.
а значит не подходит.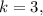 тогда
тогда 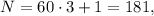 но
но 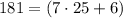 не делится на
не делится на  а значит не подходит.
а значит не подходит.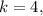 тогда
тогда 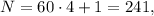 но
но 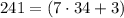 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 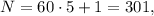 и
и 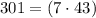 – делится на
– делится на  а значит подходит !
а значит подходит !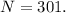
 где
где  – некоторое целое число.
– некоторое целое число.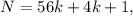 где
где  – некоторое целое число.
– некоторое целое число.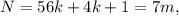 где
где  и
и 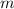 – некоторые целые числа.
– некоторые целые числа.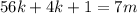 ;
;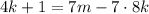 ;
;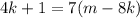 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: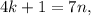 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.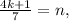 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 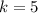 ;
;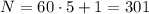 ;
; где
где  – некоторое целое число.
– некоторое целое число.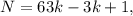 где
где  – некоторое целое число.
– некоторое целое число. где
где  и
и 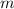 – некоторые целые числа.
– некоторые целые числа.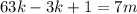 ;
;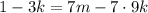 ;
;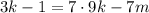 ;
;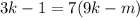 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: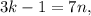 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.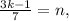 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 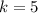 ;
;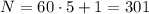 ;
;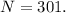
69.3 км
Пошаговое объяснение:
Давайте розрахуємо, яку відстань мотоцикліст проїхав за перші дві години, а потім віднімемо цю відстань від загальної відстані, щоб знайти відстань, яку він проїхав за третю годину.
За першу годину мотоцикліст проїхав 30% всього шляху, тобто 0.3 * 180 км = 54 км.
За другу годину він проїхав 0.45 від того, що залишилося. Щоб знайти, що залишилося, від загальної відстані віднімемо відстань, яку він вже проїхав за першу годину: 180 км - 54 км = 126 км.
Тоді він проїхав 0.45 * 126 км = 56.7 км за другу годину.
Загалом, за перші дві години він проїхав 54 км + 56.7 км = 110.7 км.
Щоб знайти відстань, яку він проїхав за третю годину, від загальної відстані 180 км віднімемо відстань, яку він вже проїхав: 180 км - 110.7 км = 69.3 км.
Отже, мотоцикліст проїхав 69.3 км за третю годину.