Завод за три дня изготовил 198 станков; причем в первый день завод изготовил в 2 раза больше станков, чем во второй день. В третий день столько станков сколько за первые два дня.
Условие:
За 1 день - 2 части, ? станков
За 2 день - 1 часть, ? станков
За 3 день - ? частей, ? станков
1) За 3 день частей (по условию - столько же, сколько за первые два дня в сумме):
1 + 2 = 3 (части)
2) Всего частей:
1 + 2 + 3 = 6 (частей)
3) На одну "часть" приходится станков:
198 : 6 = 33 (станка)
Значит, во второй день изготовили 33 станка.
4) В первый день:
33 * 2 = 66 (станков)
5) В третий день:
33 * 3 = 99 (станков)
ответ: 66 - в первый; 33 - во второй; 99 - в третий.
 день
день  станков,
станков,  день
день 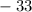 станка,
станка, 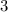 день
день 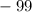 станков.
станков.
арифметический, 1-4 классы).
Во второй день завод изготовил  часть, тогда в первый день завод изготовил
часть, тогда в первый день завод изготовил  части. Т.е. за первые
части. Т.е. за первые  дня:
дня: 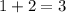 части.
части.
Т.к. 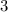 день
день  день
день  день
день 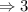 день
день 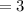 части.
части.
Значит 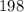 станков
станков  частей
частей 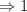 часть
часть 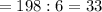 станка.
станка.
Т.к. во второй день завод изготовил  часть, то в этот день было изготовлено
часть, то в этот день было изготовлено  станка.
станка.
В первый день завод изготовил  части
части 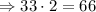 станков.
станков.
Т.к. 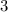 день
день  день
день 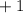 день
день 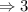 день
день  станков.
станков.
==============================================================
алгебраический, 5-9 классы).
Пусть  станков было изготовлено во второй день, тогда в первый
станков было изготовлено во второй день, тогда в первый 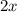 станков, а в третий
станков, а в третий 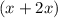 станков. Всего изготовлено
станков. Всего изготовлено 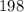 станков.
станков.
Этап 1. Составление математической модели:
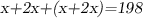
Этап 2. Работа с математической моделью:
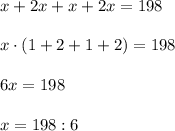
Этап 3. ответ математической модели:
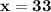
Итак, если во второй день было изготовлено 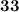 станка, тогда в первый
станка, тогда в первый 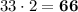 станков, а в третий
станков, а в третий 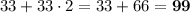 станков.
станков.
1.
(2/3 - 1/4) : 1/12
Спочатку ми виконаємо дію всередині дужок:
(2/3 - 1/4) = (8/12 - 3/12) = 5/12
Тепер ми можемо переписати вираз як:
5/12 : 1/12
Для ділення дробів ми можемо помножити перший дріб на обернений другого дробу:
(5/12) * (12/1) = 5
Тому відповідь: 5.
2.
x + 5 / y - 2 = 4
(x + 5)(y - 2) = 16
Можна вирішити цю систему рівнянь методом підстановки. З першого рівняння ми можемо виразити x:
x + 5 = 4(y - 2)
x = 4(y - 2) - 5
Тепер ми можемо підставити це значення x у друге рівняння:
(4(y - 2) - 5 + 5)(y - 2) = 16
4(y - 2)(y - 2) = 16
(y - 2)(y - 2) = 4
(y - 2) = ±2
Таким чином, ми отримали два значення для y: 4 та 0. Підставляючи їх у перше рівняння, ми можемо знайти відповідні значення x:
- Якщо y = 4:
x + 5 / 4 - 2 = 4
x + 5 / 2 = 4
x + 5 = 8
x = 3
- Якщо y = 0:
x + 5 / 0 - 2 = 4
Ця рівність не має розв'язку, оскільки ділення на 0 не визначене.
Отже, відповідь: (x, y) = (3, 4).