Пошаговое объяснение:1) f(x)= 2x²-3x+1 , [-1;1] ⇒ f'(x)= 4x-3, найдём критические точки: 4х-3=0, ⇒ х = 3/4=0,75 ∈[-1;1]. Найдём значения функции в критической точке и на концах данного промежутка: f(3/4)= 2·(3/4)²- 3·3/4 +1 =9/8 -9/4 + 1 = -1/8 ; f(1) = 0; f(-1)=6 ⇒ max f(x)=f(-1)=6; minf(x)=f(3/4)=-1/8
2)f(x)=3x²-4 на [2;4] ⇒ f'(x)=6x 6x=0, x=0-крит. точка, но x=0∉ [2;4] ⇒ Найдём значения функции на концах данного промежутка: f(2)= 3·2²-4= 12-4=8 f(4)=3·4² - 4= 48-4=44 ⇒ max f(x)=f(-4)=44; minf(x)=f(2)=8 3)f(x)=x²-1 на [0;3]⇒ f'(x)=2x , 2x=0 x=0 -критическая точка х=0 ∈ [0;3]. Найдём значения функции в критической точке и на концах данного промежутка: f(0) =0²-1=-1; f(3)=3²-1=8 ⇒max f(x)=f(3)=8; minf(x)=f(0)= -1
№ 1
Примем объем заказа за 1,
тогда за один час работы первый мастер выполняет 1/12 часть заказа,
а второй мастер - 1/15 часть заказа.
Работая совместно за один час работы мастера выполнят:
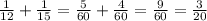 - всего заказа.
- всего заказа.
Весь заказ- 100%.
Найдем процент выполненного заказа за один час совместной работы мастеров:
100% : 20 * 3 = 15%
Значит, не больше 15% заказа мастера выполнят за 1 час совместной работы.
ответ: нет.
№ 2
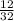
Сократим данную дроб.
Наибольший общий делитель НОД (12; 32) = 4
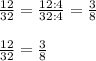
ответ: В 3/8.
№ 4

Приведём данную дробь к знаменателю 18:
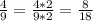
Дроби 17/18 и 11/18 не подходят, так как больше дроби 8/18.
Дроби 1/3 и 2/3 приведём к дробям со знаменателем 9:
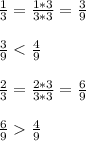
ответ: В 1/3.
3t^2+2t-1=0
t=1/3(-1+-2)
t1=-1 2x=-П/2+2Пk x=-П/4+Пk
t2=1/3
x=1/2arcsin(1/3)
2) sqrt(x-5)=3-sqrt(10-x)
x-5=9+10-x-6sqrt(10-x)
6sqrt(10-x)=24-2x
3sqrt(10-x)=12-x
9*(10-x)=144+x^2-24x
x^2-15x+54=0
x=(15+-3)/2
x1=9 x2=6