Базис. Векторы a и b образуют базис, поскольку на плоскости (у векторов по две координаты) любые два линейно независимых вектора образуют базис (поскольку пространство двумерно), а линейная независимость на плоскости эквивалентна условию, что векторы непараллельны, т.е. их координаты непропорциональны. Впрочем, можно подойти и формально, записав линейную комбинацию векторов a и b, а также приравняв её к нулю:
где - числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
Разложение. Чтобы найти разложение вектора c по базису, приравняем линейную комбинацию векторов a и b к вектору c:
Домножим левую и правую часть слева на обратную матрицу коэффициентов векторов:
Е - единичная матрица, можно опустить (получается при перемножении матрицы и обратной к ней).
Итак,
Значит, .
Прямой проверкой можно убедиться в правильности ответа:
Дано; Январь=31день; без ветра и снега= 12 дней; ветер=14 дней; снег=11дней; метель= снег + с ветром=?дней; 1)31-12=19дней или снег или ветер; 2) 19-14=5дней остаётся когда нет ветра, значит эти дни снег; 3) 11-5=6дней это снег шёл в дни с ветром, значит метель; ответ: 6дней была метель в январе; Можно так; 1) 31-12=19дней снег или ветер или метель; 2) 14+11=25 дней всего вместе снег или ветер или метель; дней всего 19, значит один и тот день идёт снег и ветер; 3)25-19=6дней метель, совпадают дни снега и ветра. Или так 1)31-14-11=6дней останется для без снега и ветра; но их по условию 12; 2)12-6=6 дней метель, потому что эти дни совпадать ветер и снег будут; Или с икс; Х=метель; 31-12+х=14+11; 19+х=25; Х=25-19; Х=6 метель; проверка 31-12+6=14+11; 25=25; ОТВЕТ: метель 6дней.
Пошаговое объяснение:
Базис. Векторы a и b образуют базис, поскольку на плоскости (у векторов по две координаты) любые два линейно независимых вектора образуют базис (поскольку пространство двумерно), а линейная независимость на плоскости эквивалентна условию, что векторы непараллельны, т.е. их координаты непропорциональны. Впрочем, можно подойти и формально, записав линейную комбинацию векторов a и b, а также приравняв её к нулю:
где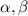 - числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
- числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
Разложение. Чтобы найти разложение вектора c по базису, приравняем линейную комбинацию векторов a и b к вектору c:
Домножим левую и правую часть слева на обратную матрицу коэффициентов векторов:
Е - единичная матрица, можно опустить (получается при перемножении матрицы и обратной к ней).
Итак,
Значит,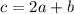 .
.
Прямой проверкой можно убедиться в правильности ответа: