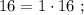
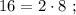
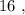т.е.: 
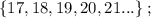
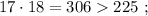
каждое – будет, очевидно, больше чем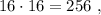 
т.е. больше 
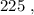а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.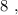
т.е.: 
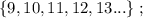
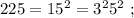
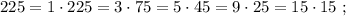
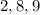и 
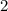и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы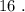 
и никаких натуральных чисел нет. и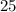 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы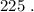 
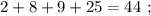
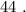
а) две окружности равны если, их радиусы равны. Окружность - это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии R (называемый радиусом) от некоторой точки, которая называется центром окружности. Диаметр (d=2·R), длина (C=2·π·R=π·d) окружности и площадь (S=π·R²) круга, ограниченной окружностью однозначно определяются через радиус. Равносильны утверждения: две окружности равны если, их радиусы или диаметры или длины окружности или площади круга, ограниченные окружностями равны.
б) два квадрата равны, если их стороны равны. Квадрат - это четырёхугольник, у которого все углы равны и все стороны равны a. Диагональ (d=a√2), периметр (P=4·a) и площадь (S=a²) квадрата однозначно определяется через его сторону. Равносильны утверждения: два квадрата равны, если их стороны или диагонали или периметры или площади равны.
в) два прямоугольника равны, если их длины и ширины равны. Прямоугольник - это четырехугольник, у которого все углы прямые. У прямоугольника противоположные стороны попарно параллельны. Длиной прямоугольника называют длину a более длинной пары его сторон, а шириной - длину b более короткой пары сторон, то есть прямоугольник определяется через два параметра. Поэтому не верно, например, утверждение: два прямоугольника равны, если их периметры равны. Так как периметр прямоугольника P=2·(a+b), то если P=10 см, то могут быть много вариантов, например, a=2 и b=3 или a=1 и b=4.