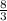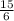.
. Готово.
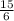и , где числитель дроби — общее число бросков, а ее знаменатель — число попаданий. Видно, что при одинаковом числе попаданий, второй баскетболист совершил меньше бросков, а значит и его результат лучше.
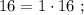
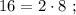
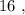т.е.: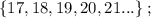 
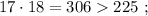
каждое – будет, очевидно, больше чем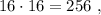 
т.е. больше 
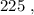а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.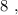
т.е.: 
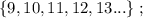
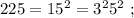
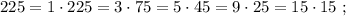
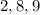и 
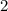и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы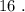 
и никаких натуральных чисел нет. и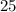 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы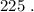 
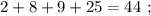
Пусть последовательность 1,2,3,4,5,6
Числа 5 и 6 - взаимно простые и НОК(5,6)=30, что удовлетворяет условию!
Остальные числа от 1 до 4 имеют наименьшее общее кратное меньше 30, это можно легко заметить по разложению чисел
1
2- простое
3- простое
4=2*2
3- простое
5- простое
6=2*3
ответ: да такая последовательность существует и равна 1,2,3,4,5,6