Пусть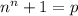 
простое число, большее 2 (если 
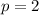, то 
). То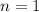гда 
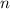четно. Заметим, что 
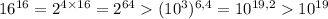, случай с 18-ю уже очевидно не подходит. Возможные кандидаты: четные числа от 2 до 16.
Согласно малой теореме Ферма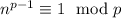 
, вместе с тем 
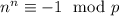. Сложив оба сравнения, получим 
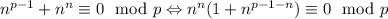, откуда ясно, что 
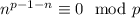. Эта процедура похожа на алгоритм Евклида. Повторив такую операцию еще несколько раз, получим 
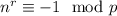, где 
определяется так: 
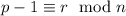. Но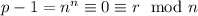 
, то есть 
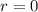. Тогда 
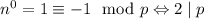, противоречие.
Есть еще случай, когда, производя операцию (алгоритм Евклида), мы не приходим к 0 (попадаем в цикл). Это происходит тогда и только тогда, когда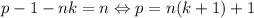 
. Небольшая проверка дает 
: 
.
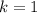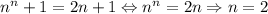ответ: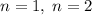 
Представим себе последовательность прямоугольных треугольников в системе координат. Ровно один катет треугольника вертикален и ровно один горизонтален. Пусть каждый треугольник "цепляется" вершиной за предыдущий так, что гипотенузы треугольников образуют монотонно снижающуюся ломаную. Тогда неравенство очевидно: кратчайший путь есть отрезок между верхней вершиной первого треугольника в последовательности и нижней вершиной нижнего. Равенство достигается тогда, когда треугольники попарно подобны.
Предположим обратное.
Заметим, что все 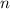, такие что 
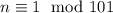не подходят. Поскольку 101 является простым, то 
взаимно просто со 101. Значит,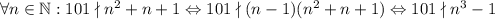 
.
Более того, согласно малой теореме Ферма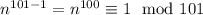 
. Значит, порядок числа 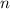по модулю 101 делит как 3, так и 100, но 3 и 100 взаимно просты. Противоречие.
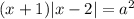
Первый аналитический)
1) Если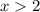 
, то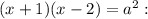 
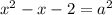
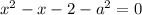
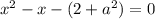
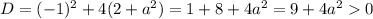
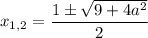
Проверим условие 
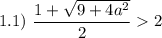
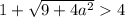
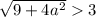
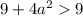
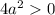
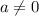
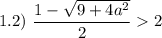
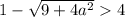
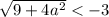
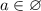
Таким образом, если 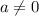, то имеем корень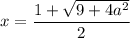 
2) Если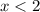 
, то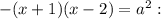 
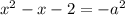
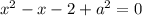
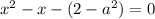
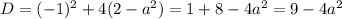
Найдем такие значения 
, при которых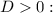 
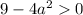
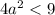
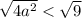
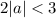
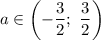
Тогда корни:
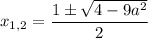
Проверим условие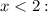 
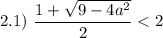
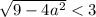
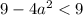
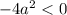
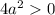
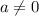
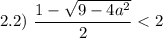
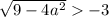
![a \in \left[-\dfrac{3}{2}; \ \dfrac{3}{2} \right]](/tpl/images/1359/4428/7966b.png)
С учетом 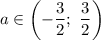имеем: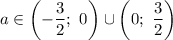 
Таким образом, при 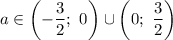имеем три корня.
Второй графический)
Рассмотрим две функции:
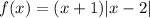
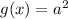— линейная функция, график — прямая, параллельная оси абсцисс
Изобразим на координатной плоскости функцию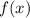 
1) Если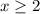 
, то 
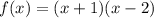— квадратичная функция, график — парабола, ветви параболы направлены вверх
2) Если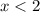 
, то 
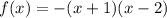— квадратичная функция, график — парабола, ветви параболы направлены вниз
Вершина параболы: 
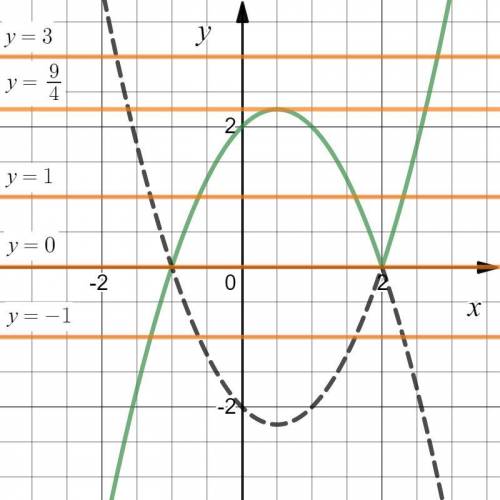
Изобразим данные функции на соответствующих участках (см. вложение).
Уравнение 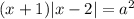будет иметь три корня, если будет три пересечения графика функции 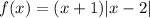c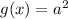
Так будет, ес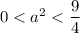ли 
или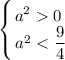 
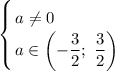
Решением системы будет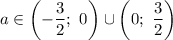
Таким образом, при 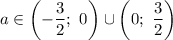имеем три корня.
ответ: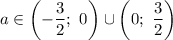
7+5=12 всего