Для упрощения выражения 5x2 + (3 - 5x)(x + 11) мы начнем с того, что вспомним шаги ,которые мы должны пройти.
Итак, мы должны выполнить открытие скобок, а затем сгруппируем и выполним приведение подобных слагаемых.
Для открытия скобок применим правило умножения скобки на скобку:
5x2 + (3 - 5x)(x + 11) = 5x2 + 3 * x + 3 * 11 - 5x * x - 5x * 11 = 5x2 + 3x + 33 - 5x2 - 55x;
Скобки открыты и мы переходим к группировки и приведению подобных:
5x2 - 5x2 + 3x - 55x + 33 = x(3 - 55) + 33 = -52x + 33.
ответ: -52x + 33.
Пошаговое объяснение:
Sбок = 32(1 + √2) см²
Пошаговое объяснение:
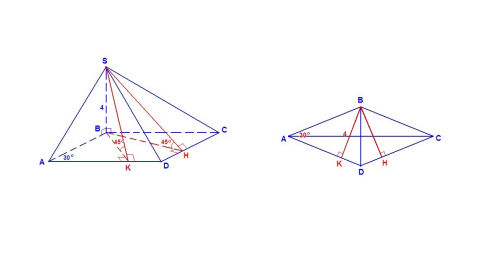
Если две грани пирамиды перпендикулярны плоскости основания, то их общее ребро перпендикулярно плоскости основания.
Пусть ребро SB⊥(АВС). SB - высота пирамиды. Тогда
(SAB)⊥(ABC) и (SBC)⊥(ABC)
Если ребро SB перпендикулярно основанию, то оно перпендикулярно каждой прямой, лежащей в основании:
SB⊥AB, SB⊥BC, значит ∠АВС = 150° - линейный угол двугранного угла между гранями SAB и SBC.
Тогда ∠BAD в ромбе равен 30° (так как сумма углов, прилежащих к одной стороне ромба, равна 180°).
Проведем ВК⊥AD и ВН⊥CD. ВK и ВH - проекции наклонных SK и SH на плоскость основания, значит
SK⊥AD, SH⊥CD по теореме о трех перпендикулярах.
Тогда ∠SKB = ∠SHB = 45° - линейные углы двугранных углов наклона двух других боковых граней к плоскости основания.
SB = 4 см.
Так как треугольники SBK и SBH прямоугольные, равнобедренные, то ВК = ВН = SB = 4 см, а SK = SH = 4√2 см (как гипотенузы равнобедренных треугольников).
ΔАВК: (∠ВКА = 90°) ВК = 4 см, ∠А = 30°, тогда АВ = 2ВК = 8 см (по свойству катета, лежащего напротив угла в 30°).
Ssba = Ssbc = 1/2 · AB · SB = 1/2 · 8 · 4 = 16 см²
Ssad = Sscd = 1/2 · AD · SK = 1/2 · 8 · 4√2 = 16√2 см²
Sбок = Ssba + Ssbc + Ssad + Sscd = 2 · 16 + 2 · 16√2 = 32(1 + √2) см²
Составим пропорцию
1 пачка-1/600ч
х пачек-1 ч
1/600х=1
х=600 пачек за 1 час
За t часов будет расфасовано 600t.