Две прямые в пространстве паралельны если они лежат на одной плоскости и не пересекаются.
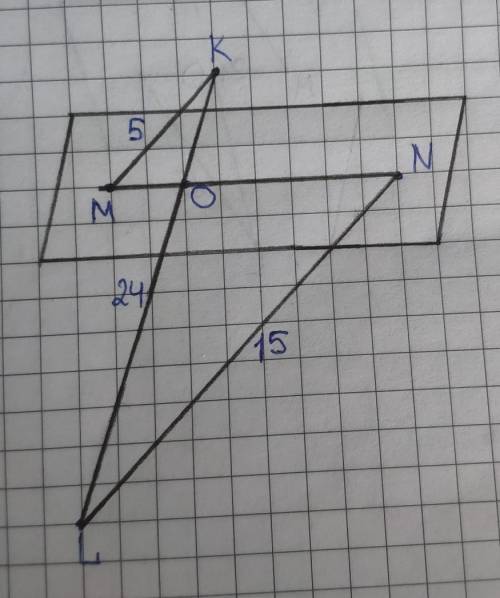
Так как MK||NL, то они лежат на одной плоскости, пусть эта плоскость – плоскость а.
Так как точки M, K, N, L принадлежат плоскости а, то прямые KL u MN так же лежат на ней.
Рассмотрим ∆MOK и ∆NOL.
KL=24 дм по условию, пусть КО=х дм, тогда LO=24–x.
Угол MOK=угол NOK как вертикальные,
Угол MKL=угол NLK как накрест-лежащие при параллельных прямых MK и NL и секущей KL.
Тогда ∆MOK~∆NOK по двум равным углам.
Стороны подобных треугольников пропорциональны.
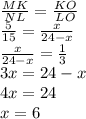
То есть KO=6 дм, LO=24–6=18 дм.
ответ: 6 дм, 18 дм.
№1
Дано:
∆АВС – равносторонний,
SC=12,
AB=4,
Углы SCA и SCB – прямые.
Найти: SA, SB
Так как ∆ABC – равносторонний по условию, то АС=ВС=АВ=4.
Углы SCA и SCB – прямые по условию, тогда ∆SCA u ∆SCB – прямоугольные.
По теореме Пифагора в ∆SCA:
SA²=SC²+AC²
SA²=12²+4²
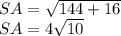
По теореме Пифагора в ∆SCB:
SB²=SC²+BC²
SB²=12²+4²
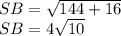
ответ: 4√10.
№2
Дано:
∆АВС – равнобедренный с основанием CD (не равносторонний так как CE≠CD),
CE=ED=10 см,
CD=16 см,
SE=2 см,
Угол SEO=90°,
ЕО – высота ∆АВС.
Найти: SO
Высота равнобедренного треугольника, проведенная к основанию, так же является медианой.
Следовательно ЕО – медиана, значит CO=DO=0,5CD=16*0,5=8 см.
Так как ЕО – высота, то угол ЕОС=90°, тогда ∆ЕОС – прямоугольный.
В ∆ЕОС по теореме Пифагора:
ЕС²=СО²+ЕО²
10²=8²+ЕО²
ЕО²=100–64
ЕО=√36
ЕО=6 см
Так как угол SEO=90° по условию, то ∆SEO – прямоугольный.
В ∆SEO по теореме Пифагора:
SO²=SE²+EO²
SO²=2²+6²
SO²=4+36
SO=√40
SO=2√10 см.
ответ: 2√10 см.
х-8=256
х=264
2)4х-32=64
4х=64+32
х=96:4
х=24
3)х-8=16
х=24
4)х-8=256
х=264
1 и 4;2 и 3 равные