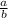 +
+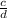 =
= 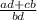
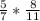 =
= 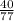
 =
= 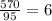
Для удобства записи будем считать, что заданы точки плоскости:
A(–6;1; –5), B(7; –2; –1) и C(10; –7;1), и точка S(3;–4; –6).
Плосокость ABC задана точками A(xa, ya, za), B(xb, yb, zb), C(xc, yc, zc).
Координаты точки A:
xa = -6
ya = 1
za = -5.
Координаты точки B:
xb = 7
yb = -2
zb = -1.
Координаты точки C:
xc = 10
yc = -7
zc = 1.
Задана точка S(xs, ys, zs).
Координаты точки S:
xs = 3
ys = -4
zs = -6.
Точка M лежит на плосокости ABC.
Отрезок SM перпендикулярен плосокости ABC.
Точка M является проекцией точки S на плосокость ABC.
Найти координаты точки M(xm, ym, zm) и длину отрезка SM.
Для нахождения координат точки M(xm, ym, zm) составим систему из трёх уравнений с тремя неизвестными, исходя из следующих трёх условий.
Точка M лежит в плоскости ABC;
Отрезок SM перпендикулярен прямой AB;
Отрезок SM перпендикулярен прямой AC.
Это равносильно трём условиям:
Смешанное произведение векторов AM, AB, AC равно нулю: AM •[ABxAC] = 0
Скалярное произведение векторов SM и AB равно нулю: SM • AB = 0
Скалярное произведение векторов SM и AC равно нулю: SM • AС = 0
Решая эту систему, найдём координаты точки M(xm, ym, zm).
Плоскость ABC задана тремя точками:
A(-6, 1, -5)
B(7, -2, -1)
С(10, -7, 1)
Задана точка S(3, -4, -6)
Проекция точки S на плоскость ABC имеет координаты M(xm, ym, zm)
xm = 7056 / 3528 = 2.
ym = -10584 / 3528 = -3.
zm = -7056 / 3528 = -2.
|SM| = sqrt(224042112) / 3528 = 4,24264.
Это расстояние было найдено по формуле:
|SM| = sqrt((xm-xs)*(xm-xs)+(ym-ys)*(ym-ys)+(zm-zs)*(zm-zs)).
Координаты векторов AB, AC, AS равны:
AB = (13, -3, 4).
AC = (16, -8, 6).
AS = (9, -5, -1).
Координаты векторного произведения AB и AC
[ABxAC] = (14, -14, -56).
Модуль векторного произведения AB и AC
|[ABxAC]| = sqrt(3528) = 59,39697.
Модуль смешанного произведения AS, AB, AC
|AS[ABxAC]| = 252.
Расстояние от точки S до плоскости ABC вычисляется по формуле
|SM| = |AS[ABxAC]| / |[ABxAC]|.
|SM| = 252 / sqrt(3528) = 3 * sqrt(2) = 4,24264.
Найдены координаты проекции точки S на плоскость ABC:
M(2, -3, -2).
Точка Р(3;–4; –6).
Теперь находим симметричную точку Q по фоормуле Q = 2M - P.
ответ: Q(1; -2; 2)
признаки делимости:
на «2» – (если число оканчивается чётной цифрой);
на «3» – (если сумма цифр числа делится на 3);
на «4» – (если две последние цифры в записи числа образуют двузначное число, кратное 4);
на «5» – (если число оканчивается 0 или 5);
на «8» – (если три последние цифры в записи числа образуют трёхзначное число, кратное 8);
на «9» – (если сумма цифр числа делится на 9);
на «10» – (если число оканчивается 0).
И ещё вопрос: что такое и как найти значения 1!, 2!, 3!, 4!, 5!, 6!, … Посмотрите, как изменяется последняя цифра числа
n! = 123456…n – произведение первых n натуральных чисел.
1! = 1
2! = 12 = 2
3! = 123 = 6
4! = 1234 = 24
5! = 12345 = 120
6! =123456 = 720 и т.д.
При n≥5 число n! всегда оканчивается нулём.