Такс, ну я попробую, хз что получится. Я так то в седьмом классе)
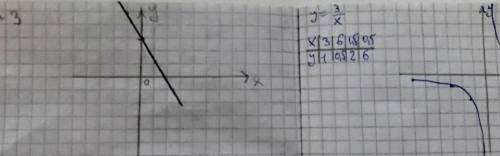
2. (пикчу прикрепил)
а) Это график обычно линейной функции
б) А это уже график обратной пропорциональности (гипербола)
3.
а) Возводим все в квадрат. 2 переносим.
x + 4 = x^2
Теперь чертим график y = x^2 (парабола) и график y = x + 4 (линейная функция). Точки пересечения - это и есть наши x. Если потом влом не будет, может нарисую.
б) Выносим x
x(x^2 + 2) + 3 = 0
3 переносим, делим все на x
x^2 + 2 = -3/x
Снова чертим график параболы (x^2 + 2) и гиперболы (-3/x). Находим точки пересечения, это и есть значение x. Думаю все это и сам умеешь, но опять же, может потом начерчу.
Напоминаю, что график гиперболы y = -3/x будет проходить в правой верхней (2) четверти и в левой нижней (4)!
4.
Выносим x
x(x + 5)
x ≠ 0 (т.к. на ноль делить нельзя).
x ≠ -5
Любое другое значение нас устраивает.
x ∈ (-∞; -5) v (-5; 0) v (0; +∞)
p.s. Извини, что так долго. Отвлечься пришлось)
Знак неравенства меньше нуля, значит, нужно, чтоб квадратичная функция была расположена ниже оси абсцисс. Для этого требуется установить направление ветвь параболы. Очевидно, же что, когда ветви параболы направлены вниз и D<0(дискриминант меньше нуля), неравенство выполняется для всех действительных значения х.
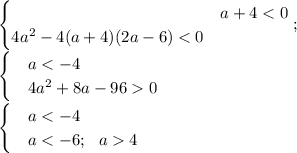
Получаем решение системы неравенств 
. То есть, при a ∈ (-∞;-6) неравенство (a+4)x²-2ax+2a-6<0 верно при всех действительных значения х. Наибольшее целое значение параметра а: а = -7.
50%от15 =7.5. И от 45. =22.5