Пошаговое объяснение:
возьмем число n ∈ N запишем произведение этого числа следующего за ним(n+1). Затем прибавим к произведению большее из этой пары:
a) n*(n+1)+n+1=n^2+2+n+1=(n+1)^2
пример: числа 6 и 7
6*7+7=49 и 7^2=49
б) n^3 - (n+1)^3=n^3-(n^+3n^2+3n+1)=n^3-n^3-3n^2-3n-1=
=3n^2+3n+1=3n(n+1)+1
[3n(n+1)+1] :3=n(n+1)+1/3
т.е. при делении на 3 получаем остаток 1. Следовательно: число не делится на три нацело.
Пример: числа 5 и 6
5^3=125; 6^3=216 216-125=91 91:3=30 и 1 в остатке
в) Нечетное число запишем, как 2n+1, где n ∈ N, тогда:
(2n+1)^2=4n^2+4n+1=4n(n+1)+1
[4n(n+1)+1]:8=[4n(n+1)+1]:4:2
Число n(n+1) – всегда четное, т.е. делится на 2 без остатка, т.е. число 4n(n+1) делится на 4*2 без остатка, а в остатке 1!
Пример: число 7 (нечетное); 7^2=49; 49:8=6*8 ост.1.
ответ: 200 км.
Пошаговое объяснение:
Весь путь разделён на 3 части: 8/20, 7/20 и 50 км. То есть, кроме 50 км, у нас есть ещё
пути.
Весь путь равен 20/20 (=1; мы поделили его на 20 частей, взяли все эти части и получился весь путь). Тогда 50 км составляют
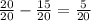
50 км =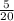 
пути. Разделим обе части равенства на 5 (и получим при этом верное равенство):
10 км = 
пути.
Одна двадцатая часть — 10 км. Семь двадцатых частей в семь раз больше, чем одна двадцатая часть:
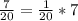
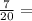10 км * 7 = 70 км.
Восемь двадцатых частей в восемь раз больше, чем одна двадцатая часть:
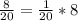
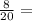10 км * 8 = 80 км.
Обозначим весь путь за s. Тогда
s=I часть + II часть + III часть
s = 80 км + 70 км + 50 км = 200 км.
ответ: 200 км.
8*12=96 кг
5*12=60 кг крупного
3*12=36 кг мелкого
60+36=96 кг всего