27
Пошаговое объяснение:
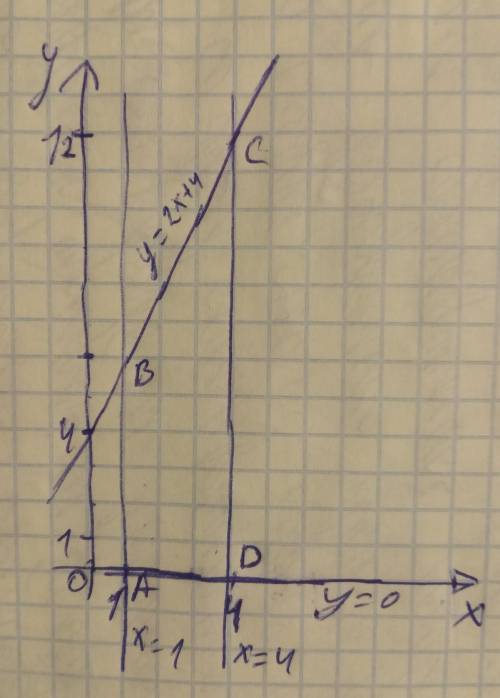
построим заданную фигуру. на рисунке указаны прямые у=2х+4, у=0 (она же ось х), х=1 и х=4 (две вертикальные линии). они образуют трапецию ABCD. точка А имеет координаты (1;0), точка D имеет координаты (4;0) это точки пересечения вертикальных линий с осью х.
найдём координаты точек В и С.
координата х точки В = 1
подставим в уравнение прямой: у = 2х+4 = 2*1+4 = 6
т.е. координаты точки В (1;6)
так же найдём координату у точки C
y = 2x+4 = 2*4+4 = 12
координаты точки C (4;12)
площадь получившейся трапеции можно найти по формуле (AB+CD)*AD/2, поскольку АВ и CD являются основаниями, а сторона AD является также высотой трапеции (потому что ось х перпендикулярна прямым х=1 и х=4)
АВ = 6; CD= 12; AD =3
(6+12)*3/2 = 27
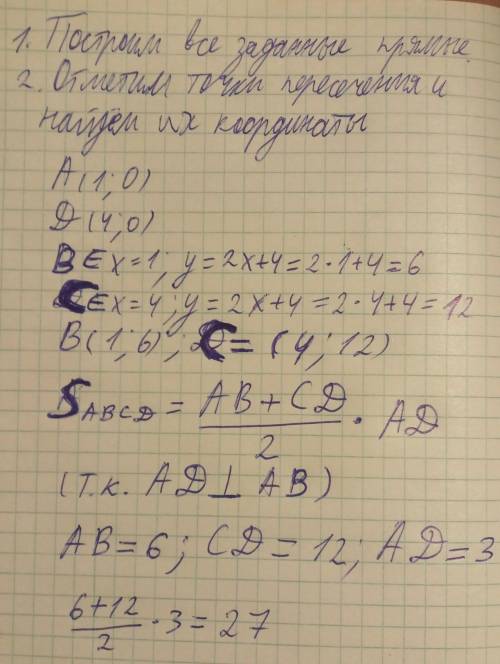
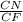 ⇒СF =
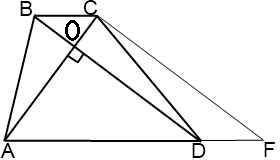
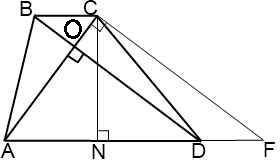
⇒СF = 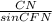 ⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S =
⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S = 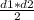 *sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m =
*sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m = 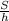 m =
m = 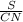 m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго... 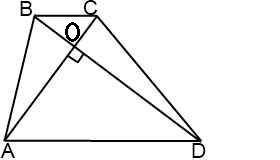
х-15,7=15,1*5,14
х-15,7=77,614
х=77,614+15,7
х=93,314
(93,314-15,7):5,14+1,45=16,55
16,55=16,55