Рассмотрим случай разрезания стола по диагонали. Пусть стол представляет собой некоторый n-угольник.
1) Количество диагоналей многоугольника, проведенных из одной вершины = n-3;
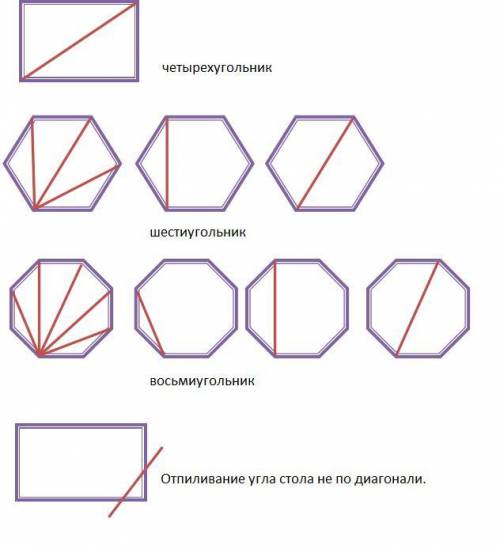
Например, у четырехугольника (n=4) 1 диагональ, у шестиугольника (n=6) 3 диагонали, у восьмиугольника (n=8) 5 диагоналей, проведенных из одной вершины.
2) При разрезании n-угольника по любой из них получаем две фигуры с общим количеством вершин = n+2.
Например.
При разрезании четырехугольника по диагонали получим 2 треугольника. Всего вершин у полученных фигур = 6; 6 = 3+3.
При разрезании шестиугольника по любой диагонали получим 2 фигуры с общим количеством вершин = 8, 8 = 3+5 = 4+4 (треугольник и пятиугольник или два четырехугольника).
При разрезании восьмиугольника по любой диагонали получим 2 фигуры с общим количеством вершин = 10; 10 = 3 + 7 = 4 + 6 = 5+5.
3) Т.о. при разрезании многоугольника по одной диагонали, получим фигуру с меньшим числом вершин, чем у исходного многоугольника на величину от 1 до n-3, т.е. получим многоугольники с количеством вершин = 3, 4, 5…, n-1.
При разрезании угла стола не по диагонали: количество углов у большей части стола увеличится на 1 по сравнению с исходным многоугольником.
1751:5≠35(ост1)
_1751⊥5
15 350
-25
25
1
Проверим: 350×5+1=1750+1=1751
ответ: 1751:5=350 (ост. 1)
1983:9≠22 (ост. 3)
_1983⊥9
18 220
-18
3
Проверим: 220×9+3=1980+3=1983
ответ: 1983:9=220 (ост.3)
2930:7≠41 (ост. 6)
_2930⊥7
28 418
-13
7
-60
56
4
Проверим: 418×7+4=2926+4=2930
ответ: 2930:7 = 418 (ост.4)
40202:6≠670 (ост. 2)
_40202⊥6
36 6700
-42
42
0
2
Проверим: 6700×6+2=40200+2=40202
ответ: 40202÷6=6700 (ост. 2)