Будем считать все переменные неотрицательными, но помнить, что если (x,y,z) - решение, то можно приписывать минусы к любой переменной, и тоже получать решение
Вынесем полные квадраты
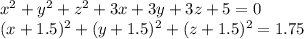
Так как прибавление 1.5 не меняет рациональности, можно рассмотреть эквивалентную задачу в рациональных числах
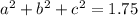
Так как a,b,c - рациональные дроби, у них существует наименьший возможный общий знаменатель, обозначим его Q. После домножения на него уравнение примет вид
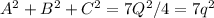(1)
Мы сразу видим, что Q четно, то есть Q=2q, а значит хотя бы одно из A,B или С нечетно, иначе Q - не наименьший возможный общий знаменатель.
Теперь отметим, что при делении на 8 квадрат целого числа дает в остатке либо 0 и 4 (если число четно), либо 1, если число нечетно.
Следовательно, возможные остатки при делении на 8 у левой части уравнения это 0, 4 и 7
Сумма трех квадратов может иметь такие остатки при делении на 8 только в следующих случаях (с учетом до перестановки)
0+0+0 -> 0, 0+0+4 -> 0, 0+4+4 -> 0, 4+4+4-> 4,
0+0+1 -> 1, 1+4+4 -> 1.
При этом остаток 7 не достигается. Первые 4 варианта не подходят, так как это означало бы что A,B,C все четны, значит остается такой вариант
Из трех A,B,C одно и только одно нечетно. Пусть это будет число C. Тогда
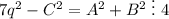
Квадраты нечетных чисел при делении на 4 дают остаток 1, четных - 0. Значит левая часть имеет остаток при делении на 4 равный либо 2 (при нечетных q) либо 3 (при четных q). Получаем противоречие, из которого делаем окончательный вывод.
Исходное уравнение не имеет решений в рациональных числах
966
Пошаговое объяснение:
Пусть всего черных шаров 420x. Тогда всего белых шаров 1.15 * 420x = 483x.
В первой коробке 2/3 всех черных шаров (2/3 * 420x = 280x штук) и 1/7 всех белых шаров (1/7 * 483x = 69x), всего 280x + 69x = 349x шаров.
Во второй коробке оставшиеся шары, их (420 + 483 - 349)x = 554x штук.
Прикинем, какой может быть знаменатель у x (очевидно, x - рациональное число).
69x должно быть целым, так что знаменатель x - делитель 69. 280x - тоже целое, тогда знаменатель x - делитель и 280. Но 69 и 280 взаимно просты, тогда знаменатель у x равен 1, x - целое.
Нужно найти такое целое число, что 349x < 1000 и 554x > 1000.
Второе неравенство в целых числах имеет решением 
, первое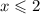 
, так что 
.
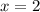Получается, что белых шаров в обеих коробках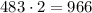 
.
3х-х=8
2х=8
Х=4