66
Количество чисел от 1 до 100 равно 100.
Из них, числа делящиеся на 5: 5, 10, 15,..., 100. Всего их 20. Объяснение:
5, 10, 15,..., 100 - арифметическая прогрессия с первым членом а₁=5, последним членом аₙ= 100 и разностью прогрессии d=5.
aₙ=a₁+d(n-1)
100=5+5(n-1)
95=5(n-1)
n-1=19
n=20
Числа первой сотни делящиеся на 7: 7, 14, 21,..., 98. Всего их 14.
Объяснение:
7, 14, 21,..., 98 - арифметическая прогрессия с первым членом а₁=7, последним членом аₙ= 98 и разностью прогрессии d=7.
aₙ=a₁+d(n-1)
98=7+7(n-1)
91=7(n-1)
n-1=13
n=14
Итак, чтобы найти количество чисел от 1 до 100 которые не делятся ни на 5 ни на 7, надо от 100 вычесть количество чисел, делящееся на 5, а также, количество чисел, делящееся на 7.
Получим 100-20-14=66
68
Пошаговое объяснение:
Из первых 100 чисел на 5 делится каждое пятое число. Таким образом количество чисел, делящихся на 5 — целая часть от частного 
т. е. 20.
Из первых 100 чисел на 7 делится каждое седьмое число. Таким образом количество чисел, делящихся на 7 — целая часть от частного 
т. е. 14.
Среди чисел, которые мы уже только что подсчитали, есть те, которые встречаются в обоих списках, т. е. делящиеся и на 5, и на 7 одновременно, а значит и на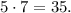 
Их количество — целая часть частного 
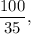т. е. 2.
Значит количество чисел, которые не делятся ни на 5, ни на 7, равно
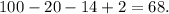
б)НОК(11,110)=110
в)НОК(26,52)=52
г)НОК(11,23)=253
д)НОК(88,66)=264
е)НОК(198,9)=198