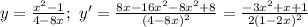
Для того чтобы найти промежутки возрастания и убывания необходимо взять производну от даннйо функции и решить следующие неравенства
y'(x)<0 при х удовлетворяющих этому неравнетсву функция убывает
y'(x)>0 при х удовлетворяющих этому неравенству функция возрастает
Найдем y'(x)=(0.5cos(x)-2)'=-0.5sin(x)
Теперь решим неравенство:
-0.5sin(x)<0 или оно эквивалентно следующему неравенству:
sin(x)>0
Это неравенство имеет решения при
Значит на этих интервалах функция убывает.
Теперь рассмотри неравенство -0.5sin(x)>0 оно эквивалентно неравенству:
sin(x)<0
И имеет следующие решения:
Значит на этих интервалах функция возрастает.
На границах интервалов функция имеет точку перегиба.
Функция y=0,5cos(x)-2 возрастает при
Убывает при
И имеет точки перегиба при
Подробнее - на -
Пошаговое объяснение:понял??? Ето жтак леко!!!
Приведем к общему знаменателю.
1) 2/7 = 90/315; 3/5 = 189/315; 4/9 = 140/315
2/7 < 4/9 < 3/5
2) 2/3 = 8/12; 3/4 = 9/12; 7/12
7/12 < 2/3 < 3/4
3) 3/4 = 105/140; 2/5 = 56/140; 4/7 = 80/140
2/5 < 4/7 < 3/4
4) 7/15 = 140/300; 7/20 = 105/300; 9/25 = 108/300
7/20 < 9/25 < 7/15
Посчитано в уме, без калькулятора!