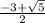4 решения:
(sqrt(1,5);2,5+2*sqrt(1,5))
(-sqrt(1,5);2,5-2*sqrt(1,5))
(sqrt(0,5),1,5+2*sqrt(0,5))
(-sqrt(0,5),1,5-2*sqrt(0,5))
Пошаговое объяснение:
ОДЗ проверим получив решения.
Второе уравнение при выполнении ОДЗ
равносильно
у-4х=(2+2х-у)^2/y
y^2-4ху=(2+2х-у)^2
y^2-4ху=4+y^2+4x^2+8x-4y-4xy
0=4+4x^2+8x-4y
y=(x+1)^2
2x-y=2x-x^2-2x-1=-x^2-1
3^(2x-y)=(1/3) 3^(-x^2)
Обозначим 3^(х^2)=a
9/a+a=4*sqrt(3)
a^2-4*sqrt(3)*a+9=0
По теореме Виета а1=3*sqrt(3) а2=sqrt(3)
Значит х^2=1,5 или х^2=0,5
Пусть х=sqrt(1,5)
тогда у1=(1+sqrt(1,5)):2=2,5+2*sqrt(1,5)
По ОДЗ подходит 2,5-2*sqrt(1,5)>0
Если х=-sqrt(1,5), то
у=(1-sqrt(1,5))^2=2,5-2*sqrt(1,5) убеждаемся, что по ОДЗ подходит.
Пусть х=sqrt(0,5)
y=1,5+2*sqrt(0,5) по ОДЗ подходит
Пусть х=-sqrt(0,5)
у=1,5-2*sqrt(0,5) по ОДЗ подходит
Итак, 4 решения:
(sqrt(1,5);2,5+2*sqrt(1,5))
(-sqrt(1,5);2,5-2*sqrt(1,5))
(sqrt(0,5),1,5+2*sqrt(0,5))
(-sqrt(0,5),1,5-2*sqrt(0,5))
ответ: 1) 1
2)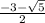
3)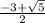
Пошаговое объяснение:
x^4+x^3-4x^2+x+1=0 Заметим, что сумма коэффициентов равна 0, значит первый корень уравнения 1, тогда можно сгруппировать уравнение как: (x-1)(x^3+2x^2-2x-1)=0
во второй части также сумма коэффициентов равна 0, значит также выносим (x-1): (x-1)^2(x^2+3x+1)=0
D=3^3-4*1*1=9-4=5
x=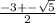
ответ: 1) 1
2)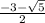
3)