Question

Найти полный дифференциал функции z=sqrt(y) * arcsin x^2 z=sin x^2 + cos^2 (x)

Answer 1

ответ: $z=\frac{2x\sqrt{y} }{\sqrt{1-x^4} }dx +\frac{arcsin(x^2)}{2\cdot\sqrt{y}}dy$

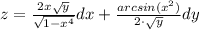
dz = (2x·cos(x²) - sin(2x))dx

Пошаговое объяснение:

Найти полный дифференциал функции  

z = √(y)·arcsin(x²)

Формула полного дифференциала функции:

$dz=\frac{\partial z}{\partial x}dx +\frac{\partial z}{\partial y}dy$

Найдем частные производные

$\frac{\partial z}{\partial x}=(\sqrt{y}\cdot arcsin(x^2))' =\sqrt{y}\cdot(arcsin(x^2))'=\sqrt{y}\cdot\frac{1}{\sqrt{1-x^4} }\cdot (x^2)'=\frac{2x\sqrt{y} }{\sqrt{1-x^4} }$

$\frac{\partial z}{\partial y}=(\sqrt{y}\cdot arcsin(x^2))' =(\sqrt{y})'\cdot arcsin(x^2)=\frac{1}{2\cdot\sqrt{y}}\cdot arcsin(x^2)=\frac{arcsin(x^2)}{2\cdot\sqrt{y}}$

$z=\frac{2x\sqrt{y} }{\sqrt{1-x^4} }dx +\frac{arcsin(x^2)}{2\cdot\sqrt{y}}dy$

Найти полный дифференциал функции  

z = sin(x²) + cos²(x)

Так как функция  z зависит только от одной переменной то формула полного дифференциала

$dz=\frac{\partial z}{\partial x}dx$

Находим производную

z' = (sin(x²) + cos²(x))' = cos(x²)·(x²)' + 2cos(x)·(cos(x))' = 2x·cos(x²) - 2sin(x)·cos(x) = 2x·cos(x²) - sin(2x)

dz = (2x·cos(x²) - sin(2x))dx