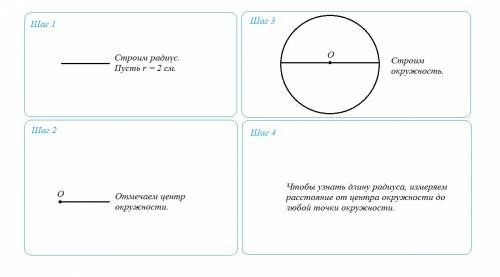
1) Строим отрезок, равный радиусу. Например, 2 см. То есть r = 2 см.
2) Отмечаем центр окружности (им будет край отрезка).
3) Измеряем циркулем отрезок, проводим окружность. Раствор циркуля должен оставаться неизменным.
4) Прикладываем линейку к радиусу и "продлеваем" его до пересечения с окружностью.
5) Чтобы узнать длину радиуса, нужно измерить расстояние от центра окружности до любой точки окружности.
упрощённый)
1) Берем произвольную длину радиуса. Пусть r = 2 см.
2) Так как радиус равен половине диаметра, то получаем следующее (вместо r подставляем значение радиуса):
d = 2r ⇒
d = 2·2 = 4 (см) - длина диаметра.
3) Отмечаем центр отрезка (диаметра). Это будет центр окружности.
Пусть O – центр окружности.
4) Строим окружность с центром в точке О.
5) Чтобы узнать длину радиуса, измеряем расстояние от центра окружности до любой точки окружности.
S круга = пи*r^2
Значит, по этой формуле, чтобы вычислить площадь, нужно знать радиус. Радиус составляют половину диаметра, значит он равен 14 дм.
Получается, площадь этого круга равна:
14^2 * пи=196 * пи
Но нам нужны две седьмые площади, значит нужно умножить это выражение на 2/7 (/ это черта дроби)
196 * пи * 2/7= 56 * пи. Это и будет две седьмые площади круга. Если нужно приблизительное значение, то пи примерно равен 3,14
56 * 3,14=175,84 дм^2
ответ: приблизительно 175,84 дм^2.