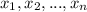 называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулю:
называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулю: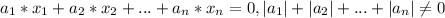
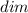 ) пространства.
) пространства. 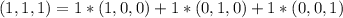
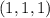 - есть линейная комбинация этих 3-х векторов.
- есть линейная комбинация этих 3-х векторов.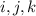 ).
).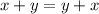 ;
;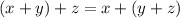 ;
;1 см³ - 100 мм³ = 1.000 мм³ - 100 мм³ = 900 мм³ = 0,9 см³
1 дм³ - 200 см³ = 1 дм³ - 0,2 дм³ = 0,8 дм³
100 м² + 2 га = 100 м² + 20.000 м² = 20.100 м²
800 а : 2 = 400 а
1 000 см³ - 1 дм³ = 1.000 см³ - 1.000 см³ = 0 см³
400 м² : 4 = 100 м²
200 дм³ + 100 м³ = 200 дм³ + 100.000 дм³ = 100.200 дм³
10 см³ + 1.000 см³ = 1.010 см³
5 м³ : 100 дм³ = 5.000 дм³ : 100 дм³ = 50 дм³ = 0,05 м³
500 м³ + 100 дм³ = 500.000 дм³ + 100 дм³ = 500.100 дм³ = 500,1 м³
5 м³ + 100 дм³ = 5.000 дм³ + 100 дм³ = 5.100 дм³ = 5,1 м³
50 м² + 100 дм² = 5.000 дм² + 100 дм² = 5.100 дм² = 50,1 м²
Смотрим сперва на Дану. Он говорит то, что заведомо невозможно: если Вану рыцарь, то Ану и Бану лжецы(см. слова Вану). Значит, Дану - лжец.
Теперь рассмотрим оставшихся трех по отдельности. Если Вану рыцарь, то Ану и Бану лжецы, значит, рыцарь один.
Если Бану рыцарь, то Вану лжец (он сказал что Бану лжец, а тот в нашем допущении рыцарь), кроме того, Ану тоже лжец - также он противоречит сказанному Бану, опять рыцарь один.
Если предположить что Ану рыцарь, то также видно что Вану и Бану лжецы, рыцарь один.
Значит, кто бы из этих троих не был бы рыцарем, он будет только один.
Предположим теперь, что они все лжецы.
Вану лжец, значит, раз он солгал, как минимум один из Ану и Бану - рыцарь, что противоречит нашему предположению, следовательно, рыцарь есть, и он только один.