Сократите, , дроби,если они сократимы: 14/30; 45/120; 24/84; 40/240; 1980/3960; 15/120; 224/1120

👇

Ответ:

lenya013

08.08.2022

14\30=7\15 сократили на 2
45\120=3\8 сократили на 15
24\84=2\7 сократили на 12
40\240=1\6 сократили на 40
1980\3960=1\2 сократили на 1980
15\120=1\8 сократили на 15
224\1120=1\5 сократили на 224.

4,6(15 оценок)

Ответ:

erika20122003

08.08.2022

14/30=не сокращается
45/120=15/40=3/8
24/84=12/42=6/21=2/7
40/240=10/60=2/12=1/6
1980/3960=990/1980=495/990=99/198=33/66=11/22
15/120=3/24
224/1120=112/560=56/280=7/35

4,6(42 оценок)

Открыть все ответы

Ответ:

marinamax2004

08.08.2022

Пошаговое объяснение:

1 . 3,(05) = 3,050505... = 3 + 0,05 + 0,0005 + . . . = 3 + 0,05/( 1 - 0,01 ) =

= 3 + 0,05/0,99 = 3 + 5/99 = 3 5/99 ;

0,(6) = 0,6666... = 0,6/( 1 - 0,1 ) = 0,6/0,9 = 6/9 = 2/3 ;

- 0,(8) = - 0,8/0,9 = - 8/9 ;

0,(057) = 0,057/0,999 = 57/999 = 19/333 ;

1,(55) = 1 + 0,55/0,99 = 1 55/99 = 1 5/9 .

2 . 12,(273) = 12 + 273/999 = 12 273/999 = 12 91/333 ;

0,11(6) = 0,11 + 0,006/0,9 = 11/100 + 6/900 = 11/100 + 2/300 =35/300 = 7/60 ;

0,0(01) = 0,0010101... = 0,001/0,99 = 1/990 .

3 . 0,0023 = 2,3 * 10⁻³ ; 5103,01 = 5,10301 * 10³ .

4,4(13 оценок)

Ответ:

PaFaS123

08.08.2022

Действия:

1) Произведения корней одинаковой степени равно корню произведения. Запишем число в виде степени с основанием 5.

2) Сократим числа на наибольший общий делитель 8.

3) Умножим числа.

4) Упростим корень.

5) Умножим дробь на 5/5 (для умножения двух дробей нужно умножить числитель и знаменатель отдельно). Произведение корней одинаковой степени равно корню произведения.

6) Запишем число в виде степени с основанием 5. Вычислим произведение.

7) Сократим степень корня и показателя степени на 2. После на 4.

Альтернативный вид первого выражения = 0,89 = 0,9.

Решение для второго:

1) Избавимся от иррациональности в знаменателе.

2) Запишем повторяющееся умножения в показательной форме.

3) Используя (a-b)^2=a^2-2ab+b^2, запишем выражение в развернутом виде.

4) Складываем. Вынесем за скобки общий множитель 2.

5) Сократим дробь на 2.

6) Поскольку сумма двух противоположных величин равно нулю, убираем их. Складываем остаток.

Решение для третьего:

1) Представим смешанную дробь в виде неправильной дроби.

2) Упростим выражение.

3) Вычислим произведение.

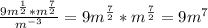
$\frac{9m^{\frac{1}{2} }*m^{\frac{7}{2} } }{m^{-3} } =9m^{\frac{7}{2} } *m^{\frac{7}{2} } =9m^{7}$

Пошаговое объяснение:

$\frac{\sqrt[4]{\frac{5}{8}*128 } }{\sqrt[4]{5^{3} } }=\frac{\sqrt[4]{5*16} }{\sqrt[4]{5^{3} } } =\frac{\sqrt[4]{80} }{\sqrt[4]{5^{3} } }= \frac{2\sqrt[4]{5} }{\sqrt[4]{5^{3} } }= \frac{2\sqrt[4]{5} }{\sqrt[4]{5^{3} } }*\frac{\sqrt[4]{5} }{\sqrt[4]{5} }=\frac{2\sqrt[4]{25} }{\sqrt[4]{5^{3}*5 } }=\frac{2\sqrt[4]{5^{2} } }{\sqrt[4]{5^{4} } } =\frac{2\sqrt{5} }{\sqrt[4]{5^{4} } } =\frac{2\sqrt{5} }{5}$

$\frac{(\sqrt{5}-\sqrt{3})*(\sqrt{5}-\sqrt{3}) }{2}+\frac{\sqrt{5}+\sqrt{3} }{\sqrt{5}-\sqrt{3} } =\frac{(\sqrt{5}-\sqrt{3})*(\sqrt{5}-\sqrt{3}) }{2}+\frac{(\sqrt{5}+\sqrt{3})*(\sqrt{5}+\sqrt{3}) }{2}=\frac{(\sqrt{5}-\sqrt{3}) ^{2} }{2} +\frac{(\sqrt{5}+\sqrt{3})*(\sqrt{5}+\sqrt{3}) }{2}= \frac{(\sqrt{5}-\sqrt{3}) ^{2} }{2}+\frac{(\sqrt{5}+\sqrt{3}) ^{2} }{2}=\frac{5-2\sqrt{15}+3 }{2}+\frac{(\sqrt{5}+\sqrt{3}) ^{2} }{2}= \frac{5-2\sqrt{15}+3 }{2}+\frac{5+2\sqrt{15}+3 }{2}=$ $=\frac{8-2\sqrt{15} }{2} +\frac{5+2\sqrt{15}+3 }{2}=\frac{8-2\sqrt{15} }{2}+\frac{8+2\sqrt{15} }{2}=\frac{2(4-\sqrt{15}) }{2}+\frac{8+2\sqrt{15} }{2}= \frac{2(4-\sqrt{15}) }{2}+\frac{2(4+\sqrt{15}) }{2}= 4-\sqrt{15} +\frac{2(4+\sqrt{15}) }{2}=4-\sqrt{15} +4+\sqrt{15}=4+4=8$