если квадратный трехчлен aх2+bx+c представлен в виде a(х+p)2+q, где p и q — действительные числа, то говорят, что из квадратного трехчлена выделен квадрат двучлена.
покажем на примере как это преобразование делается.
выделим из трехчлена 2x2+12x+14 квадрат двучлена.
вынесем за скобки коэффициент a, т.е. 2:
2
x
2
+
12
x
+
14
=
2
(
x
2
+
6
x
+
7
)
преобразуем выражение в скобках.
для этого представим 6х в виде произведения 2*3*х, а затем прибавим и вычтем 32. получим:
2
(
x
2
+
2
⋅
3
⋅
x
+
3
2
−
3
2
+
7
)
=
2
(
(
x
+
3
)
2
−
3
2
+
7
)
=
=
2
(
(
x
+
3
)
2
−
2
)
=
2
(
x
+
3
)
2
−
4
т.о. мы выделили квадрат двучлена из квадратного трехчлена, и показоли, что:
2
x
2
+
12
x
+
14
=
2
(
x
+
3
)
2
−
4
разложение на множители квадратного трехчлена
если квадратный трехчлен aх2+bx+c представлен в виде a(х+n)(x+m), где n и m — действительные числа, то говорят, что выполнена операция разложения на множители квадратного трехчлена.
покажем на примере как это преобразование делается.
разложим квадратный трехчлен 2x2+4x-6 на множители.
вынесем за скобки коэффициент a, т.е. 2:
2
x
2
+
4
x
−
6
=
2
(
x
2
+
2
x
−
3
)
преобразуем выражение в скобках.
для этого представим 2х в виде разности 3x-1x, а -3 в виде -1*3. получим:
=
2
(
x
2
+
3
⋅
x
−
1
⋅
x
−
1
⋅
3
)
=
2
(
x
(
x
+
3
)
−
1
⋅
(
x
+
3
)
)
=
=
2
(
x
−
1
)
(
x
+
3
)
т.о. мы разложили на множители квадратный трехчлен, и показоли, что:
2
x
2
+
4
x
−
6
=
2
(
x
−
1
)
(
x
+
3
)
заметим, что разложение на множители квадратного трехчлена возможно только тогда, когда, квадратное уравнение, соответсвующее этому трехчлену имеет корни.
т.е. в нашем случае разложить на множители трехчлен 2x2+4x-6 возможно, если квадратное уравнение 2x2+4x-6 =0 имеет корни. в процессе разложения на множители мы установили, что уравнение 2x2+4x-6 =0 имеет два корня 1 и -3, т.к. при этих значениях уравнение 2(x-1)(x+3)=0 обращается в верное равенство
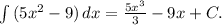
336:48*100=700 км - весь путь
700-336=364 км - в первый день