1) y''-3y'
Решение уравнения будем искать в виде 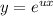 . Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами.
. Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами.
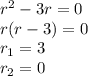
Тогда систему составят функции:
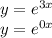
Общее решение однородного уравнения: 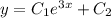 , где C ∈ R
, где C ∈ R
2) 2ch3x
Ищем частное решение
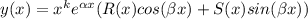
R(x) и S(x) это полиномы, их степень - макс. степень полиномов P(x) и Q(x)
У нас:
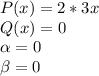
Поэтому k у нас равен 1 (т.к. 0i наш корень кратности)
И уравнение имеет частное решение
y=x(Ax+B)
Находим производные, которые нужно подставить в исходное ур.
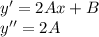
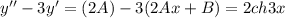
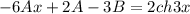
Отсюда получаем систему, приравняв коэф. при х:
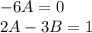
Решаем и находим корни: A=0, B=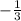
Тогда частное решение примет вид: 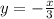
И теперь общее решение уравнения примет вид:
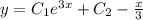
Второе решается АНАЛОГИЧНО! Пояснять решения далее не буду, все расписал в 1 примере
1)y''-3y'
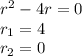
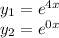
2) 16ch4x
k у нас равен 1
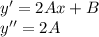
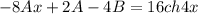
Система;
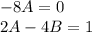
Корни:
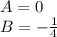
Вид частного решения: 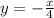
И теперь общее решение уравнения примет вид:
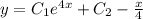
1) 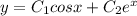
2) 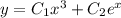
Пошаговое объяснение:
ЛОДУ 2ого порядка с переменными коэффициентами имеет вид 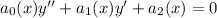
Общее решение такого ДУ - линейная комбинация двух его линейно независимых частных решений.
В обоих заданиях необходимо заметить, что сумма коэффициентов 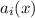 равна 0. Значит, очевидно, одним из частных решений данного ДУ будет функция
равна 0. Значит, очевидно, одним из частных решений данного ДУ будет функция 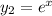 [и действительно:
[и действительно: 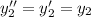 , а тогда уравнение принимает вид
, а тогда уравнение принимает вид 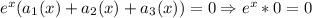 - верное равенство].
- верное равенство].
1) Рассмотрим Вронскиан системы 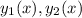 :
:
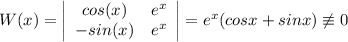
Значит, данные частные решения линейно независимы - а тогда общее решение имеет вид 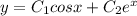 .
.
2) Очевидно искать частное решение в виде многочлена. Пусть его старший член равен 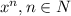 [коэффициент при старшей степени не имеет значения, т.к. уравнение однородное], т.е.
[коэффициент при старшей степени не имеет значения, т.к. уравнение однородное], т.е. 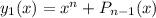 .
.
Тогда
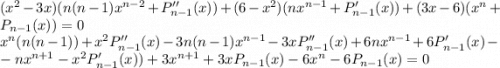
То есть коэффициент при старшей степени 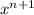 получаемого в левой части многочлена равен
получаемого в левой части многочлена равен  [степень
[степень 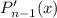 не выше
не выше 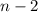 , а
, а 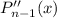 не выше
не выше 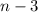 ]. Но в правой части тождественный ноль - а значит если некий многочлен и является частным решением уравнения, то это многочлен степени 3.
]. Но в правой части тождественный ноль - а значит если некий многочлен и является частным решением уравнения, то это многочлен степени 3.
Нетрудной подстановкой 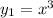 убеждаемся, что это решение ДУ:
убеждаемся, что это решение ДУ:
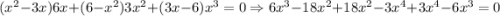 - верное равенство.
- верное равенство.
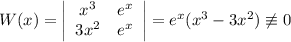
А тогда общее решение имеет вид
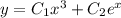
2)798дм
3)28см
4)329173(кг)