х=8
Пошаговое объяснение: х+2х+6+х=38 4х+6=38 4х=38-6 4х=32 х=8
Эти уравнения не такие страшные и сложные, какими могут показаться на первый взгляд, здесь всего-навсего нужно делать замены:
а)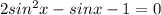 
Пусть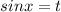 
, имеем:
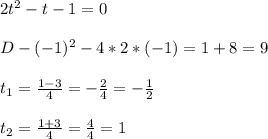
Вернёмся к замене:
Теперь найденные корни подставляем вместо t в sinx = t и ищем новые корни:
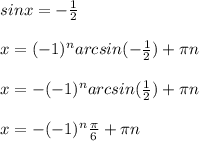
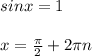
ответ: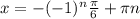 
и 
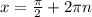
б)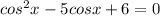 
Пусть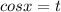 
, имеем:
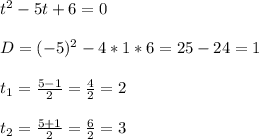
Вернёмся к замене:
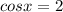
Мы знаем, что cos x не может быть больше 1 или меньше -1 (область значений: [-1; 1]), поэтому данное уравнение не имеет корней:
x ∈ ∅
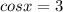
Аналогичная ситуация:
x ∈ ∅
ответ: корней нету (или x ∈ ∅, или х ∉ R)
в) 
Пусть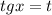 
, имеем:
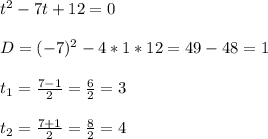
Вернёмся к замене:
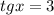
Обрати внимание на то, что тангенс может быть каким угодно числом (его область значений (-∞; +∞)), поэтому это уравнение имеет корни:
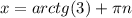
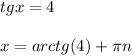
ответ: 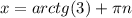и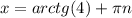 
г)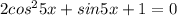 
Всю малину портит косинус, поэтому сделать замену тут нельзя. Чтобы решить эту проблему, добудем синус из косинуса по формуле: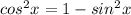 
Имеем:
Пусть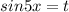 
, имеем:
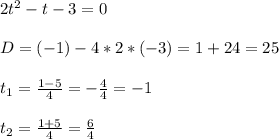
Второй корень не подходит, т.к.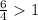 
.
Вернёмся к замене:
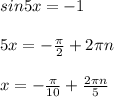
ответ: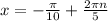 
2) 506879, 201540
3) 102680, 208970
4)100000
5)136900, 24800
6)500, 230230