Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от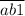 
до 
, либо от 
до 
.
Значит, в любом случае среди этих чисел есть следующие:
, делящееся на 2
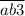, делящееся на 3
, делящееся на 4
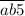, делящееся на 5
, делящееся на 6
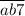, делящееся на 7
, делящееся на 8
Рассмотрим утверждение "" делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит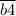 
делится на 4, 
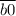делится на 4, 
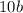делится на 4, 
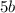делится на 2, значит 
- четное.
Рассмотрим утверждение ""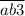 делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, 
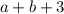делится на 3, 
делится на 3. Выпишем пары цифр, где 
, а - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение ""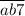 делится на 7"". Если 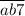делится на 7, то 
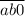делится на 7, 
делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13
При делении числа "а" на 9 получили остаток 5
Значит число а можно записать как
а=9к+5
А теперь воспользуемся свойством делимости:
"Если и уменьшаемое, и вычитаемое делятся на некоторое число, то и разность делится на это число"
запишем нашу разность
заметим, что число b тоже можно разделить на 9 с остатком
значит запишем его как
b=9n+x
и теперь наша разность будет выглядеть так
a-b=9m(9k+5)-(9n+x)=9m9(k-n)+(5-x)=9m
чтобы это равенство выполнялось x=5
И тогда число b должно делиться на 9 с остатком 5
приведем пример:
50:9= 5*9+5
41:9=4*9+5
50-41=9 и оно кратно 9
221:9=24*9+5
140:9=15*5+5
221-140=81
и оно кратно 9
