10652 - 9067 = 1585
Пошаговое объяснение:
Подай - воды = Паша
П О Д А Й
--
В О Д Ы
П А Ш А
В слове подай первая П - разряд дес. тыс. В ответе этого разряда уже нет, значит, на этом месте стояла 1, и мы её заняли, чтобы вычесть из буквы О букву В. Т.о, П =1.
1 О Д А Й
--
В О Д Ы
1 А Ш А
Из О вычли В и получили 1. Учитывая, что мы заняли 1 из предыдущего разряда, 1 в ответе можно получить, если О = 0, а В = 9.
1 0 Д А Й
--
9 0 Д Ы
1 А Ш А
Из Д вычитаем 0 и получаем А, Д могло бы быть = А, но, по условию, это невозможно: каждой букве - своя цифра.
Значит из Д занимаем 1 для разряда десятков, т.е. для А:
Д- 1 =А, Д и А отличаются на 1, и при этом А < Д на 1. Следовательно,
Д = 6, А =5
1 0 6 5 Й
--
9 0 6 Ы
1 5 Ш 5
Й - Ы = 5 , Й могло бы быть = 9, а Ы =4, но цифра 9 уже занята ( В =9), следовательно, Й < Ы .
Й не может быть =1, т.к. 1= П. Попробуем цифру 2.
Й = 2, тогда Ы =7
И так как изв разряда десятков взяли 1, то Ш = 14 - 6 = 8
Ш =8
Получили:
1 0 6 5 2 Подай
--
9 0 6 7 воды
1 5 8 5 Паша
(см. объяснение)
Пошаговое объяснение:
Приведу несколько идей к решению:
1:
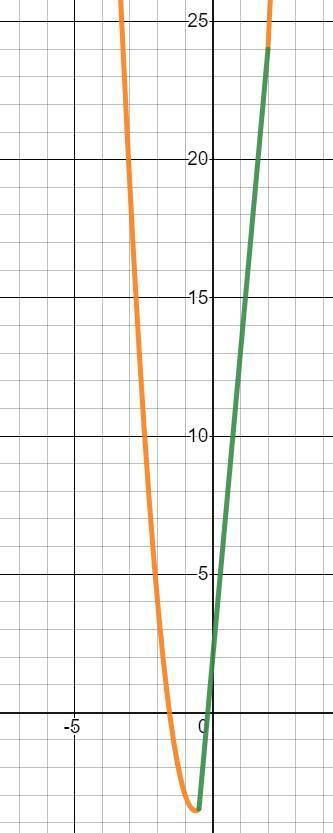
Когда видишь только буквы a (параметр) и x (переменная), то выгодно использовать достаточно универсальный прием: методику построения в координатах (x; a) /или/ (a; x). Тогда у тебя получатся парабола и прямая, склеивающиеся в общих точках (см. прикрепленный файл; построение в координатах (x; a); прямая выделена зеленым; парабола оранжевым). Теперь просто двигаешь горизонтальную прямую вверх и вниз и смотришь пересечения. Единственное решение достигается при 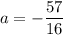 ; решений нет при
; решений нет при 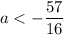 .
.
2:
Другим хорошим может стать построение левой и правой частей уравнения по-отдельности. Для левой части строим параболу 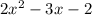 и симметрично отражаем все, что под осью x. Для правой части будет парабола, которая бегает вверх или вниз в зависимости от значения параметра. Единственное решение возможно, только когда
и симметрично отражаем все, что под осью x. Для правой части будет парабола, которая бегает вверх или вниз в зависимости от значения параметра. Единственное решение возможно, только когда 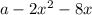 касается
касается 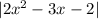 , откуда
, откуда 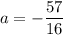 . Здесь стоит остановиться на том, как считать a:
. Здесь стоит остановиться на том, как считать a: 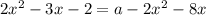 (обратите внимание, что здесь можно не писать модуль)
(обратите внимание, что здесь можно не писать модуль)  . Берем дискриминант и приравниваем к нулю:
. Берем дискриминант и приравниваем к нулю: 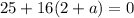 . Откуда получаем требуемое значение. Если
. Откуда получаем требуемое значение. Если 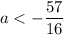 , то решений нет.
, то решений нет.
3:
Пусть 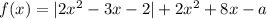 . Тогда:
. Тогда: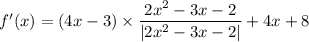 . Решив
. Решив 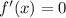 , получаем, что
, получаем, что  . Просчитав знаки, делаем вывод, что функция убывает до
. Просчитав знаки, делаем вывод, что функция убывает до  , а затем возрастает при любом значении параметра. Тогда достаточно решить
, а затем возрастает при любом значении параметра. Тогда достаточно решить 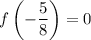 , откуда
, откуда 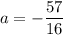 . Таким пользоваться не рекомендую.
. Таким пользоваться не рекомендую.
Задание выполнено!