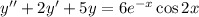
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
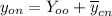
Составим однородное дифференциальное уравнение, соответствующее данному неоднородному:
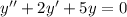
Составим характеристическое уравнение и решим его:
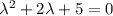
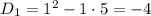
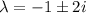
Общее решение однородного уравнения:
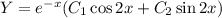
Запишем в общем виде частное решение данного неоднородного уравнения, учитывая, что в правой части стоит произведение экспоненты и на косинус, а также то, что степень экспоненты и выражение под знаком косинуса совпадают с соответствующими выражениями, полученными при решении однородного уравнения:
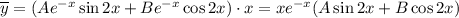
Находим первую производную:
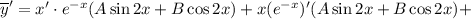
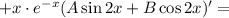
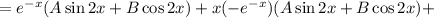
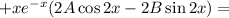
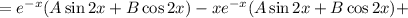
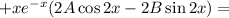
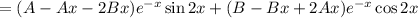
Находим вторую производную:
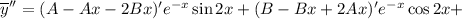
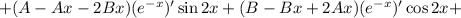
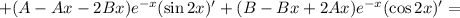
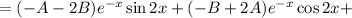

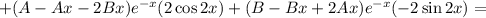
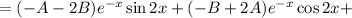
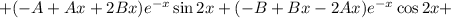
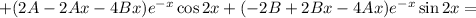
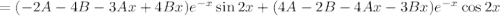
Подставляем в исходное уравнение:
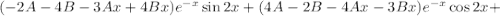
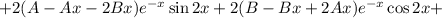
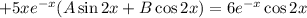
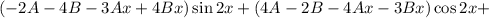
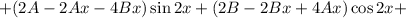
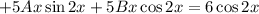
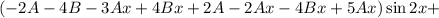
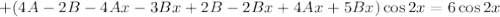
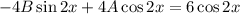
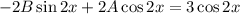
Условие равенства левой и правой частей:
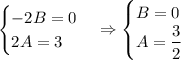
Частное решение данного неоднородного уравнения:
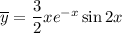
Общее решение данного неоднородного уравнения:
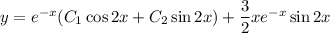
1)2sin(x) - 3 cosx = 2
4 sin(x/2)cos(x/2) - 3(cos^2(x/2) - sin^2(x/2)) = 2 (cos^2(x/2)+sin^2(x/2))
откуда
5 sin^2(x/2) - 4 sin(x/2)cos(x/2) - cos^2(x/2) = 0
делим на cos^2(x/2) , тога получим
5 tg^2(x/2) - 4 tg(x/2) - 1=0
tg(x/2) = t, 5t^2 - 4 t - 1 =0
получаем корни t1=1 бе2= -0.2
t1=1 => tg(x/2) = 1 => x/2= Pi/4 + Pi *n, => x1 = Pi/2 + 2*Pi*n
t2=-0.2 => tg(x/2) = -0.2 => x/2= - arctg(0.2) + Pi * n=> x2=-2 arctg(0.2) + 2*Pi*n
4) sqrt(cos5x+cos7x)=sqrt(cos6x)
sqrt(2cos6xcosx)=sqrt(cos6x)
|2 cos6xcosx | = |cos6x|
cos^2(6x) *(4*cos^2(x) - 1 ) =0
откуда 1) 6x= Pi/2 + Pi*n => x1 = Pi / 12 + Pi*n/6 (этот корень подходит при проверке !!)
2) 4cos^2(x) - 1 =0
cosx= 0.5 и cosx= - 0.5
cosx=0.5 => x2 = +(-) Pi /3 + 2*Pi*n (подходит! )
cosx = -0.5 => x3 = +(-) 2*Pi/3 +2*Pi*n ( этот корень не подходит приподстановке в начальное уравнение, он не является корнем нашего уравнения . )
ответ :x1= x1 = Pi / 12 + Pi*n/6, x2 = +(-) Pi /3 + 2*Pi*n
3) sin2x + sin4x + sin 6x = 1/2ctgx
sin2x +sin6x=2sin4xcos2x, тогда имеем
2 sin4xcos2x + sin4x = 0.5*tgx( заменяю 1/ctgx=tgx)
2 sin4x(2cos2x +1) = tgx (0.5 перенес в левую часть, поэтому появился множитель 2)
4sin2xcos2x(2(cos^2(x) - sin^2(x)) + 1 ) = tgx
8sinx cosx (4cos^2()x - 1 ) = tgx ( в левой части я сделал преобразования 2(cos^2(x) - sin^2(x)) + 1 = 3cos^2(x) -sin^2(x)=4cos^2(x) - 1 )
tgx=sinx/cosx, поэтому можем перенести в левую часть cosx
8sinx cos^2(x) (4cos^2(x) - 1 )=sinx
sinx(8 cos^2(x) (4cos^2(x) - 1 ) - 1)=0 (имеем два уравнения)
1)sinx=0 => x1=Pi*n
2) 8 cos^2(x) (4cos^2(x) - 1 ) - 1)=0
32 cos^4(x) - 8cos^2(x) - 1=0
cos^2(x)=t ,
32 t^2 - 8t - 1=0
корни t1 = (1+sqrt(3))/8, t2= (1 - sqrt(3))/8 (t2 <0, поэтому он нам не подходит, т. к cos^2(x)=t и cos^2(x)>0 ! )
t1 = (1+sqrt(3))/8
cos^2(x) = (1+sqrt(3))/8
cosx = +(-) sqrt((1+sqrt(3))/8)
x2=+(-) arccos(sqrt(1+sqrt(3))/8)) + Pi*n
x3=+(-) (Pi - arccos(sqrt((1+sqrt(3))/8))) )+ Pi*n ( т. к. arccos sqrt(- (1+sqrt(3))/8) = Pi - arccos sqrt(1+sqrt(3))/8) )
ответ: x1=Pi*n
x2=+(-) arccos(sqrt(1+sqrt(3))/8)) + Pi*n
x3=+(-) (Pi - arccos(sqrt((1+sqrt(3))/8))) )+ Pi*n