На 40% увеличится площадь прямоугольника, если его длину увеличить на 15%, а ширину увеличить на 22%.
Пошаговое объяснение:
Если его длину увеличить на 15%, а ширину увеличить на 22%, то:
Представим проценты в виде дроби: 0.15 и 0.22, тогда:
Длина a+0.15a = 1.15a; Ширина b+0.22b = 1.22b
S = a*b = 1.15a*1.22b = 1.4ab
Отношение площадей: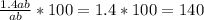 
, отнимаем от значения 100% обычной площади и получаем: 140 - 100 = 40%.
На 40% увеличится площадь прямоугольника, если его длину увеличить на 15%, а ширину увеличить на 22%.
Відповідь:Основанием прямоугольного параллелепипеда является параллелограмм со сторонами 3 м и 5 м и углом между ними 60º. Площадь большего диагонального сечения равна 63 м². Найдите площадь боковой поверхности параллелепипеда.
Решение.
Найдем площадь боковой поверхности. Нам известна площадь большего диагонального сечения. Чтобы найти площадь диагонального сечения нужно умножить высоту прямоугольного параллелепипеда на диагональ основания. Найдём диагональ основания по теореме косинусов
c²=a²+b²-2ab*cos(180-α)
c²=3²+5²-2*3*5*cos(180-60)
c²=9+25-30*cos120
c²=34-30*()
c²=34+15
c²=49
c=7 (м) -диагональ основания
Значит высота прямоугольного параллелепипеда равна
h=63:7=9 м
Значит площадь боковой поверхности равна
S=2*(ah+bh)=2*(3*9+5*9)=2*(27+45)=2*72=144 м²
б) (-0,3) в степени 3= -0.027< 0
в) -(-2 1/2) в степени 5= 3125/32 =97 21/32 > 0
г) (-1) в степени 12=1>0
д) (-1) в степени 11.=-1<0
е) -(-1/5) в степени 10=-1/9765 625 < 0
3125 32
288 97
245
224
21