Пусть х км/ч - скорость второго велосипедиста, тогда (х + 3) км/ч - скорость первого велосипедиста. 15 мин = (15 : 60) ч = 0,25 ч. Уравнение:
42/х - 42/(х+3) = 0,25
42 · (х + 3) - 42 · х = 0,25 · х · (х + 3)
42х + 126 - 42х = 0,25х² + 0,75х
0,25х² + 0,75х - 126 = 0 | разделим обе части уравнения на 0,25
х² + 3х - 504 = 0
D = b² - 4ac = 3² - 4 · 1 · (-504) = 9 + 2016 = 2025
√D = √2025 = 45
х₁ = (-3-45)/(2·1) = (-48)/2 = -24 (не подходит, так как < 0)
х₂ = (-3+45)/(2·1) = 42/2 = 21
ответ: 21 км/ч - скорость второго велосипедиста.
Проверка:
42 : 21 = 2 ч - время движения второго велосипедиста
42 : (21 + 3) = 42 : 24 = 1,75 ч - время движения первого
2 - 1,75 = 0,25 ч = (0,25 · 60) мин = 15 мин - разница
Пошаговое объяснение:
Пусть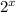 = t; t>0
= t; t>0
[tex]t^{2} -7t+10=0
D= 49-40= 9 > 0 2 различных корня
t1 = 7+3/2 = 5
t2 = 7-3/2=2
Отмечаем на координатной прямой.
t²-7t+10 это парабола. ветви вверх
Смотришь область которая ниже нуля
получается [2;5]
2^{x} = t
2^{x} ≥ 2 x= 1
2^{x} ≤5 x= ㏒₂5
ответ: [1; ㏒₂5]