Пусть скорость мотоциклиста из пункта А до В равна х км/ч
весь путь вычисляется по формуле
S=vt
Тогда время в часах затраченное мотоциклистом от А до В равно
t = S/x
а время от В до А равно
S/2÷ (x+9)+S/2÷30
так как время обратного пути мотоциклиста равно первоначальному, то получаем следующее уравнение
S/x = S/2÷ (x+9)+S/2÷30
Делим обе части уравнения на S, т.к. знаем, что S, не равно 0
переносим в одну сторону. Получаем следующее уравнение
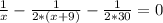
приведем к общему знаменателю
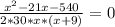
Дискриминант равен (-21)²-4*1* (-540)= 2601
Д больше 0, значит уравнение имеет 2 корня

Так как скорость не может быть отрицательным числом, значит
ответ 36 км/ч
x=1
Пошаговое объяснение:
Точка минимума - точка, в которой производная равна 0, при этом производная меняет свой знак с "-" на "+" при прохождении через эту точку
Найдём производную:
y'=3x^2-4x+1
Приравняем к 0: 3x^2-4x+1=0
x=1 и x=1/3
При x<1/3 y>0, при 1/3<x<1 y<0, при x>1 y>0 => x=1 - точка минимума
x=1 - точка минимума