Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 - 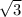
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
33 года отцу
Пошаговое объяснение:
Пусть, х - возраст отца, у - возраст сына.
Из условия:
х = у + 24
Пусть, отец достигает 4кратного возраста сына через t лет.То есть:
х + t = 4y
В этом возрасте он будет старше сына в 3 раза
х + t = 3*(y +t)
Получили систему 3 уравнений с 3 неизвестными
х = у + 24
х + t = 4y
х + t = 3*(y +t)
х = у + 24
t = 4y - х
х + t = 3y + 3t
х = у + 24
t = 4y - х
х - 3y = 3t - t = 2t
х = у + 24
t = 4y - х
х - 3y = 2*(4y-x)
Выразим х как (у + 24) в соответствии с 1м уравнением системы:
(y+24) - 3y = 2*[4y-(y+24)]
Решим уравнение:
24 - 2y = 2*(3y - 24)
24 - 2y = 6y - 48
6y + 2y = 24 + 48
8y = 72
y = 9
Найдём х:
х = у + 24 = 9+24 = 33
Следовательно
ответ: 33 года