ответ: х = –π/2 + 2 * π * k, где k – целое число.
Пошаговое объяснение:
Решим данное тригонометрическое уравнение √(2) * cos(π/4 + x) – cosx = 1 с пояснением.
К левой части уравнения применим формулу cos(α + β) = cosα * cosβ – sinα * sinβ (косинус суммы). Тогда, получим: √(2) * (cos(π/4) * cosх – sin(π/4) * sinх) – cosx = 1.
Согласно таблице основных значений синусов, косинусов, тангенсов и котангенсов, имеем: sin(π/4) = cos(π/4) = √(2) / 2. Следовательно, √(2) * ((√(2) / 2) * cosх – (√(2) / 2) * sinх) – cosx = 1. Раскроем скобки: cosх – sinх – cosx = 1 или sinх = –1.
Полученное тригонометрическое уравнение sinх = –1 имеет следующее решение: х = –π/2 + 2 * π * k, где k – целое число.
ответ: ответ №3
Пошаговое объяснение:
Вычислим в столбик первый и третий варианты ответа, получим соответственно 12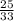
и 11
.
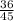Далее произведем оценку второго и четвертого вариантов:
2: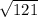 
< 
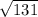, то есть данное число чуть больше 11 (т.к. 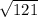= 11)
4: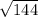 
< 
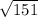, то есть данное число чуть больше 12 (т.к. 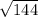= 12)
Точка А находится ближе к точке 11, визуально она соответствует числу, меньшему 12, а значит варианты 1 и 4 отпадают. Остается сравнить между собой 2 и 3 варианты:
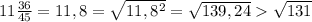
То есть третий вариант, численно равный 11,8, больше второго, и визуально ближе к середине отрезка.
