ответ:Значение побед Александра Невского
Битва за устье Невы была борьбой всей Руси за сохранение выхода к морю. Победа русских дружин под руководством Александра Невского предотвратила потерю берегов Финского залива и полную блокаду Руси. Тем самым она облегчила дальнейшую борьбу русского народа за независимость и сохранению торгового пути в страны Европы.
Победа на Чудском озере — Ледовое побоище — имела огромное значение для всей Руси, для всего русского народа и народов Восточной Европы. Впервые в истории был положен предел грабительскому продвижению на Восток, которое немецкие рыцари с папской курии осуществляли в течение нескольких столетий. Ледовое побоище сыграло решающую роль и в борьбе литовского народа за независимость. Оно вызвало широкий отклик во всех землях Прибалтики. Произошли восстания в Латвии, Пруссии, Польском В 50-х годах было заключено соглашение между Александром Невским и королем Норвегии Хоконом IV, впервые определившее русско-норвежскую границу: были признаны права Руси на Карелию и часть Финляндии.
Невская битва и Ледовое побоище явились крупной исторической вехой в развитии северо-западных земель и в целом Руси. Это еще одно свидетельство непоколебимого мужества русского народа в борьбе с иноземными захватчиками.
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
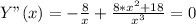
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении
