Например, 2 * 3 * 5 * 7 + 1 = 211. Число 211 само является простым.
2 * 3 * 5 * 7 * 11 + 1 = 2311. Число 2311 также простое.
[ Т. е. произведение всех подряд идущих простых чисел от первого и до определенного и плюс 1 всегда будет давать простое число? Проверяем:
2 * 3 + 1 = 7,
2 * 3 * 5 + 1 = 31.
Но если числа идут не от первого простого и не подряд, то в результате простое число не всегда получается:
3 * 5 * 7 + 1 = 106 (составное)
2 * 5 * 7 + 1 = 71 (простое)
2 * 3 * 7 + 1 = 43 (простое)
3 * 5 * 7 * 11 + 1 = 1156 (составное)
3 * 11 * 13 + 1 = 430 (составное)
2 * 3 * 11 * 13 + 1 = 859 (простое)
Получается, что число 2 в этой формуле (n = p1 * p2 * … + 1) всегда приводит к простому числу в результате, независимо от того, какие взяты остальные простые числа. Без него всегда получается составное, также независимо от того, как и каком количестве взяты простые.]
Вообще-то, то что число, полученное по формуле n = p1 * p2 * … + 1, где множество p - простые числа, начинающиеся с первого и идущие подряд, также будет простым доказывается. Ведь если n не делится ни на одно из ряда p, то нет других простых чисел до него, кроме него самого
Пошаговое объяснение:
Выясним, при каких значениях переменной функция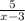 
не определена.
R ( x ) =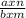 
, где n - степень числителя, а m - степень знаменателя.
Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
Если n = m , то горизонтальной асимптотой является прямая y = a b .
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m .
n = 0
m = 1
n < m , ось X, y = 0 , является горизонтальной асимптотой. y = 0
Вертикальные асимптоты: x = 3
Горизонтальные асимптоты: y = 0
Нет наклонных асимптот.
3*5=15 см
ответ:15 см площадь прямоугольника
2 задача какая то тупая ты точно ее правильно списала?