1 м = 10 дм = 100 см = 1000 мм
1 см³ = 1 см * 1 см * 1 см = 10 мм * 10 мм * 10 мм = 1000 мм³
1 дм³ = 1 дм * 1 дм * 1 дм = 10 см * 10 см * 10 см = 1000 см³
1 м³ = 1 м * 1 м * 1 м = 100 см * 100 см * 100 см = 1 000 000 см³
1 м³ = 1 м * 1 м * 1 м = 10 дм * 10 дм * 10 дм = 1000 дм³
1 дм³ = 1 дм * 1 дм * 1 дм = 100 мм * 100 мм * 100 мм = 1 000 000 мм³
1 000 000 мм³ = 1 000 000 / 1000 = 1000 см³
1000 мм³ = 1000 / 1000 = 1 см³
27 000 мм³ = 27 000 / 1000 = 27 см³
1 000 000 см³ = 1 000 000 / 1000 = 1000 дм³
64 000 см³ = 64 000 / 1000 = 64 дм³
1000 см³ = 1000 / 1000 = 1 дм³
1 000 000 см³ = 1 000 000 / 1 000 000 = 1 м³
81 000 дм³ = 81 000 / 1000 = 81 м³
1000 дм³ = 1000 / 1000 = 1 м³
1 000 000 мм³ = 1 000 000 / 1000 = 1000 см³
1 000 000 мм³ = 1 000 000 / 1 000 000 = 1 дм³
Прямоугольный ΔA₁B₁C₁ : катет A₁C₁ ---- 6 ( см ) ; катет B₁C₁ ---- 8 ( см )
Прямая треугольная призма ABCA₁B₁C₁ : боковое ребро AA₁ ---- 12 ( см )
Найти:Площадь полной поверхности данной призмы : S ( пол. пов. ) ---- ? ( см² )
Решение:Рассмотрим прямоугольный треугольник A₁B₁C₁, который лежит в основании прямой треугольной призмы ABCA₁B₁C₁:
катет A₁C₁ ---- 6 ( см ) ; катет B₁C₁ ---- 8 ( см ) - это известно по условию.
Но мы знаем, что в прямоугольном треугольнике имеются три стороны: 2 катета и гипотенуза ( наибольшая сторона ).
Вспоминаем, что: теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
Найдём гипотенузу A₁B₁ прямоугольного треугольника A₁B₁C₁ по теореме Пифагора:
c² = a² + b² ⇒ c = √(a² + b²) = √(8² + 6²) = √(64 + 36) = √100 = 10 ( см ) .
Теперь найдём площадь нашего прямоугольного треугольника у основания прямой треугольной призмы ( это и будет S основания, домноженного на 2) :
S = 1/2 * 6 * 8 = 3 * 8 = 24 ( см² ) = 24 * 2 = 48 ( см² )
Затем найдём сумму площадей прямоугольников ACA₁C₁ и BCB₁C₁ ( это же и будет площадь боковой поверхности ) :
S = 12 * (8 + 6 + 10) = 12 * 24 = 288 ( см² ) .
Остаётся найти ответ на вопрос задачи: чему равна площадь полной поверхности призмы ABCA₁B₁C₁?
S ( пол. пов. ) = 48 ( см² ) + 288 ( см² ) = 336 ( см² ).
ответ: 336 ( см² ) площадь полной поверхности призмы.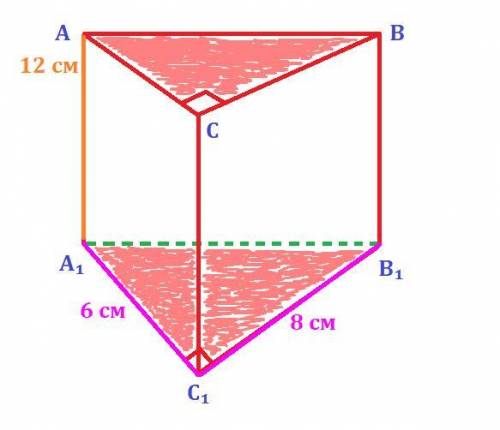
2. Er tritt in eine bereits bestehende Offene Handelsgesellschaft ein
3. Die Mitglieder einer Genossenschaft übernehmen Geschäftsanteile
4. Die Bedeutung der einzelnen Wirtschaftsbereiche verändert sich im Laufe der Zeit stark
5. Die Eigenkapitalbasis besteht nur aus dem eingelegten Vermogen des Unternehmers