2001 ^ 2001 = 1
24 ^ 21 = 4
9 ^ 20 - 7 ^ 20 = 0
8 ^ 99 = 2
3 ^ 101 = 3
549 ^ 49 = 9
2 ^ 2015 = 8
1993 ^ 1993 = 9
777 ^ 333 + 333 ^ 777 = 0
Пошаговое объяснение:
2001 ^ 2001 = 1
т.к. 1 в любой степени оканчивается 1, т.к. 1 * 1 = 1 - только один вариант последней цифры
24 ^ 21 = 4
т.к. 4 в любой степени оканчивается только на 4 и на 6, при этом нечётная степень - на 4, а чётная - на 6 оканчивается, у нас 21 - нечётное число, выбираем именно 4 на конце
9 ^ 20 - 7 ^ 20 = 0 (1 - 1 = 0)
т.к. 9 в любой степени оканчивается только на 9 и на 1, при этом нечётная степень - на 9, а чётная - на 1 оканчивается, у нас 20 - чётное число, выбираем именно 1 на конце
т.к. 7 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 7, на 9, на 3 и на 1, при этом период выбора - четыре цифры, в показателе степени 20 помещается целых пять периодов по четыре цифры, выбираем четвёртый вариант цифры окончания (на 7, 9, 3, 1) - именно 1 на конце
и, наконец, при вычитании этих двух многозначных чисел, оканчивающихся на 1, имеем 1 - 1 = 0 в конце
Аналогично рассуждаем:
8 ^ 99 = 2
т.к. 8 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 8, на 4, на 2 и на 6, при этом период выбора - четыре цифры, в показателе степени 99 помещается после целых периодов ещё три цифры, выбираем третий вариант цифры окончания (на 8, 4, 2, 6) - именно 2 на конце
3 ^ 101 = 3
т.к. 3 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 3, на 9, на 7 и на 1, при этом период выбора - четыре цифры, в показателе степени 101 помещается после 25 целых периодов по четыре цифры ещё одна цифра, выбираем первый вариант цифры окончания (на 3, на 9, на 7 и на 1) - именно 3 на конце
549 ^ 49 = 9
т.к. 9 в любой степени оканчивается только на 9 и на 1, при этом нечётная степень - на 9, а чётная - на 1 оканчивается, у нас 49 - нечётное число, выбираем именно 9 на конце
2 ^ 2015 = 8
т.к. 2 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 2, на 4, на 8 и на 6, при этом период выбора - четыре цифры, в показателе степени 2015 помещается после целых периодов по четыре цифры ещё три цифры, выбираем третий вариант цифры окончания (на 2, на 4, на 8 и на 6) - именно 8 на конце
1993 ^ 1993 = 9
т.к. 3 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 3, на 9, на 7 и на 1, при этом период выбора - четыре цифры, в показателе степени 1993 помещается после целых периодов по четыре цифры ещё две цифры, выбираем второй вариант цифры окончания (на 3, на 9, на 7 и на 1) - именно 9 на конце
777 ^ 333 + 333 ^ 777 = 0 (7 + 3 = 0)
т.к. 7 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 7, на 9, на 3 и на 1, при этом период выбора - четыре цифры, в показателе степени 333 помещается после целых периодов по четыре цифры ещё одна цифра, выбираем первый вариант цифры окончания (на 7, на 9, на 3 и на 1) - именно 7 на конце
т.к. 3 в любой степени оканчивается уже в четырёх вариантах последней цифры - на 3, на 9, на 7 и на 1, при этом период выбора - четыре цифры, в показателе степени 777 помещается после целых периодов по четыре цифры ещё одна цифра, выбираем первый вариант цифры окончания (на 3, на 9, на 7 и на 1) - именно 3 на конце
и, наконец, выполняем сложение двух многозначных чисел, одно оканчивается на 7, другое - на 3, тогда имеем: 7 + 3 = 10, т.е. оканчивается на 0.
Докажем, что пяти достаточно.
Пусть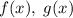 
два многочлена четвертой степени, которые совпадают в пяти точках. Тогда 
является многочленом, имеющим пять корней. Но степень многочлена
Четырех может быть недостаточно: Всего у многочлена четвертой степени пять коэффициентов, значит, пять неизвестных. Четыре уравнения не всегда дают единственное решение.
Можно доказать и более общий результат:
Если 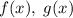— многочлены, степени 
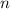, то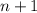 
— минимальное количество точек, в которых достаточно проверить совпадение многочленов, чтобы доказать их тождественное равенство.
База: для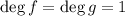 
все очевидно: по аксиоме требуется две точки для однозначного определения прямой.
Переход: пусть для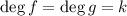 
верно. Докажем истинность для 
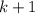. Для этого предположим обратное: достаточно 
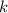точек. Возьмем различные многочлены 
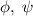степени
a^4 + 8a^2 + 16 - 16a^2 = (a^2 + 4a + 4) * (a^2 - 4a + 4)
a^ - 8a^2 + 16 = a^4 - 4a^3 + 4a^2 + 4a^3 - 16a^2 + 16a + 4a^2-16a - 16
a^4 - 8a^2 + 16 = a^ - 8a^2 + 16
a^ - 8a^2 + 16 -a^4 + 8a^2 - 16 = 0
(4a + 1)^2 * (4a - 1)^2 = (16a^2 + 1)^2 - 64a^2
(16a^2 + 8a +1) * (16a^2 - 8a + 1) = 256a^4 + 32a^2 1 - 64a^2
256a^4 - 128a^3 + 16a^2 + 128a^3 - 64a^2 + 8a + 16a^2 -8a + 1 = 256a^4 - 32a^2 + 1
256a^4 - 32a^2 + 1 = 256a^4 - 32a^2 + 1
256a^4 - 32a^2 + 1 -256a^4 + 32a^2 - 1 = 0