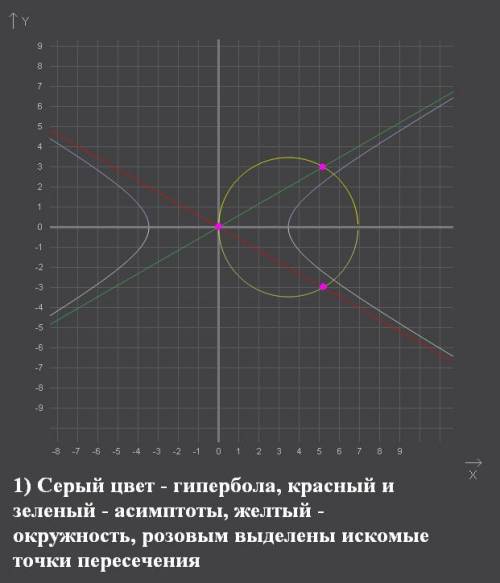
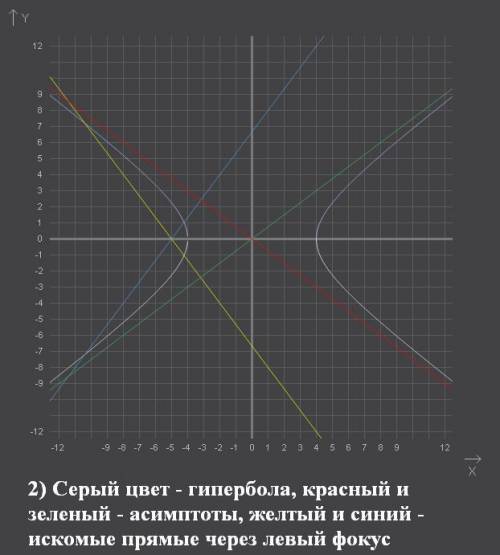
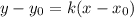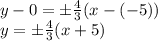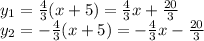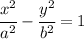Влевой части равенства надо поставить знаки действий и скобки, чтобы равенство было верным 3 3 3 3 3 3=1000

👇

Увидеть ответ

Ответ:

gzhanatugan

14.11.2020

3 3 3 * 3 + 3 : 3=1000

4,7(74 оценок)

Ответ:

Даддсаап

14.11.2020

3×3×3÷3×3-3 равно дай плюс

4,7(23 оценок)

Открыть все ответы

Ответ:

sergejryazanov228

14.11.2020

1.
Уравнение гиперболы имеет стандартный вид: $\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} =1$ , где а и b - полуоси гиперболы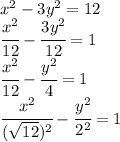
$x^2-3y^2=12 
\\\
 \cfrac{x^2}{12} - \cfrac{3y^2}{12} =1
\\\
 \cfrac{x^2}{12} - \cfrac{y^2}{4} =1
\\\
 \cfrac{x^2}{( \sqrt{12} )^2} - \cfrac{y^2}{2^2} =1$
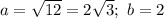
Значит, у гиперболы $a= \sqrt{12} =2 \sqrt{3} ;\ b=2$
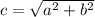
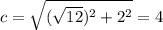
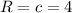
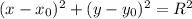Правый фокус гиперболы имеет вид F(c; 0), где $c= \sqrt{a^2+b^2}$
Находим с:
$c= \sqrt{( \sqrt{12})^2+2^2 } =4$
Так как окружность проходит через начало координат, то ее радиус равен абсциссе правого фокуса, то есть R=c=4

Общий вид уравнения окружности: (x-x_0)^2+(y-y_0)^2=R^2

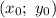, где $(x_0; \ y_0)$ - центр окружности, R - ее радиус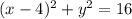
Уравнение окружности: (x-4)^2+y^2=16

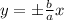
Асимптоты гиперболы имеют вид: $y=\pm \frac{b}{a} x$
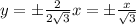
Тогда, асимптоты гиперболы $y=\pm \frac{2}{2 \sqrt{3} } x=\pm\frac{ x }{\sqrt{3}}$
Подставляем в уравнение окружности выражение для у:
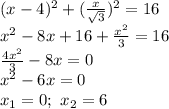
$(x-4)^2+( \frac{x}{ \sqrt{3} } )^2=16
\\\
x^2-8x+16+ \frac{x^2}{ 3} } =16
\\\
 \frac{4x^2}{ 3} }-8x =0
\\\
x^2-6x =0
\\\
x_1=0; \ x_2=6$
Тогда у для соответствующих х равны:
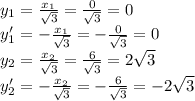
$y_1= \frac{x_1}{ \sqrt{3} } =\frac{0}{ \sqrt{3} } =0 \\\ y_1'= -\frac{x_1}{ \sqrt{3} } =-\frac{0}{ \sqrt{3} } =0 \\\ y_2= \frac{x_2}{ \sqrt{3} } =\frac{6}{ \sqrt{3} } =2 \sqrt{3} 
\\\
y_2'= -\frac{x_2}{ \sqrt{3} } =-\frac{6}{ \sqrt{3} } =-2 \sqrt{3}$
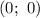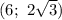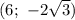
ответ: $(0; \ 0)$ ; $(6; \ 2 \sqrt{3} )$ ; $(6; \ -2 \sqrt{3} )$

2.
Так как известна одна полуось и точка, принадлежащая гиперболе, о можно найти вторую полуось:
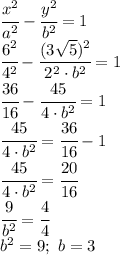
$\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} =1
\\\
 \cfrac{6^2}{4^2} - \cfrac{(3 \sqrt{5}) ^2}{2^2\cdot b^2} =1
\\\
 \cfrac{36}{16} - \cfrac{45}{4\cdot b^2} =1
\\\
 \cfrac{45}{4\cdot b^2} = \cfrac{36}{16}-1
\\\
 \cfrac{45}{4\cdot b^2} = \cfrac{20}{16}
\\\
 \cfrac{9}{b^2} = \cfrac{4}{4}
\\\
b^2=9; \ b=3$
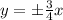
Тогда уравнения асимптот принимают вид: $y=\pm \frac{3}{4} x$
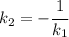
Угловой коэффициент перпендикулярной прямой является обратным и противоположным числом к угловому коэффициенту исходной прямой: $k_2=- \cfrac{1}{k_1}$
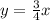Тогда, для прямой $y=\frac{3}{4}x$ таким коэффициентом является число 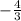$- \frac{4}{3}$ , а для прямой 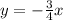$y=-\frac{3}{4}x$ - число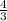 $\frac{4}{3}$
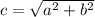
Левый фокус гиперболы имеет вид F(-c; 0), где $c= \sqrt{a^2+b^2}$
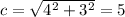$c=\sqrt{4^2+3^2} =5$ , следовательно через точку (-5; 0) нужно провести искомые прямые
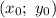Уравнение прямой, проходящей через заданную точку $(x_0; \ y_0)$ с заданным угловым коэффициентом k имеет вид: y-y_0=k(x-x_0)

Тогда:
$y-0=\pm \frac{4}{3} (x-(-5))
\\\
y=\pm \frac{4}{3} (x+5)$
Или по отдельности:
$y_1=\frac{4}{3} (x+5)=\frac{4}{3} x+ \frac{20}{3} 
\\\
y_2=-\frac{4}{3} (x+5)=-\frac{4}{3} x- \frac{20}{3}$

№1. найти точки пересечения асимптот гиперболы х²-3у²=12 с окружностью,имеющей центр в правом фокусе

№1. найти точки пересечения асимптот гиперболы х²-3у²=12 с окружностью,имеющей центр в правом фокусе

4,4(21 оценок)

Ответ:

принцеска005

14.11.2020

Давай рассмотрим на примере)
Возьмём смешанную дробь.
Сама смешанная дробь - это дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.
Например: Три целых пять седьмых.
Натуральное число - число целых, следовательно, эта смешанная дробь больше трёх, т.к. у нас есть ещё пять седьмых.
А следующее число после трёх - четыре. Но нам не хватает до четырёх ещё две седьмых. Значит, что смешанная дробь больше своей целой части, но меньше натурального числа, следующего за этой частью.

Если что-то не поняла, напиши) Постараюсь ещё чётче объяснить)

4,6(54 оценок)

Это интересно:

Компьютеры-и-электроника

21.05.2022

Как восстановить игру League Of Legends: шаг за шагом...

Хобби-и-рукоделие

23.06.2021

Как стать профессиональным игроком?...

Компьютеры-и-электроника

16.10.2021

Как использовать RealVNC: простой и эффективный способ удаленного управления компьютером...

Финансы-и-бизнес