CD = 24 см
Пошаговое объяснение:
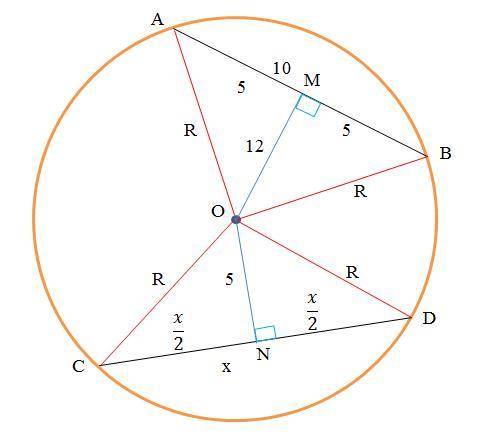
Дано (см. рисунок):
Окружность радиуса R
AB=10 см– длина первой хорды
OM=12 см– расстояние от центра O окружности до хорды AB
ON=5 см – расстояние от центра O окружности до хорды CD
Найти: x=CD – длину второй хорды.
Решение.
Так как OA=OB=OC=OD и равны радиусу R окружности, то получаем равнобедренные треугольники OAB и OCD. По условию, расстояние от центра O окружности до хорды AB, то есть длина отрезка OM, перпендикулярного к отрезке AB, равно 12 см. Точно также, расстояние от центра O окружности до хорды CD, то есть длина отрезка ON, перпендикулярного к отрезке CD, равно 5 см.
Но, по свойству равнобедренных треугольников, перпендикуляры OM и ON к основанию равнобедренных треугольников, соответственно, OAB и OCD является высотой, медианой и биссектрисой. Тогда медианы OM и ON делят, соответственно, основание равнобедренных треугольников OAB и OCD пополам. Отсюда получаем:
1) длина MB=10:2=5 см и длина ND=x:2 см;
2) треугольники OMB и OND прямоугольные с гипотенузой, равной радиусу R.
Применим теорему Пифагора к прямоугольному треугольнику OMB и находим R:
R² = OM²+MB² = 12²+5² = 144+25 = 169 = 13² или R=13 см.
Применим теорему Пифагора к прямоугольному треугольнику OCD:
R² = ON²+ND² = 5²+(x:2)² или
(x:2)² = R²–5² = 13²–5² = 169–25 = 144 = 12² или
x:2 = 12 см.
Отсюда CD=x= 12•2 = 24 см.
ответ: a) 0,3456
б) 0,68256
в) 0,92224
Пошаговое объяснение:
При решении используется формула Бернулли.
Вероятность вытянуть изделие высшего сорта p = 40% = 0,4
Вероятность не вытянуть изделие высшего сорта q = 1 - p = 1 - 0,4 = 0,6
а) A: "из пяти случайно отобранных изделий 2 высшего сорта"
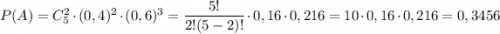
б) B: "из пяти случайно отобранных изделий не более 2 высшего сорта"
Не более двух - это 0, 1 или 2 изделия высшего сорта
C: "из пяти случайно отобранных изделий 1 высшего сорта"
D: "из пяти случайно отобранных изделий 0 высшего сорта"
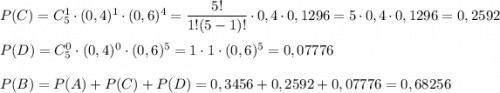
в) E: "из пяти случайно отобранных изделий хотя бы одно высшего сорта"
Найдём вероятность события E через противоположное событие D.
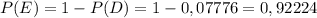
120:6=20см
20*5=100