Примем остаток денег после покупки билета на катер за 1, тогда
1) 1-3/8=5/8 - часть денег, оставшаяся после покупки открыток и она равна 35 рублей, значит всего осталось денег:
2) 35*8/5=56 (руб) - осталось после того, как купила билет на катер
3) 336-56=280 (руб.) - стоил билет на кате
ответ: На каждой чаше не более чем две гири. (по одной или по две)
Пошаговое объяснение:
Поскольку, если поменять гири с одинаковыми номерами местами, правая чаша перевешивает или сравнивается с левой, то гиря на левой чаше с n номером всегда тяжелее гири правой гири с n-м номером. (n=1,2,3...k)
Пусть:
M1n - масса n-гири в левой чаше , M2n - масса n-гири справа.
Обозначим : Xn = M1n -M2n >0
Тогда масса груза на левой чаше , на :
X= X1 + X2 + X3 ...+Xk больше чем на правой чаше.
При обмене гирь с одним номером , из разности масс X вычитается
2*M1n и прибавляется 2*M2n
X' = X1 + X2 + X3 ...+Xk -2*M1n +2*M2n = X1 + X2 + X3 ...+Xk - 2*Xn = X1 + X2 +Xn-1 -Xn + Xn+1 +Xn+2+Xk
Поскольку правая чаша перевешивает или уравнивает левую, то X'<0
(X1 + X2 +Xn-1 + Xn+1 +Xn+2+Xk) -Xn <=0
То есть это значит, что любая из взятых разностей не меньше суммы всех остальных разностей, а значит не меньше и их частичных сумм. (cумм некоторых из оставшихся)
Пусть таких разностей более 2 , то есть существует как минимум 3 разности : X1, X2,X3 , тогда
X1+X2 <=X3
X1+X3 <=X2
Сложим попарно эти неравенства :
2*X1 +X2 +X3 <= X2+X3
2*X1<=0
X1<=0
Но Xn>0
Мы пришли к противоречию , значит более двух гирь с каждой стороны быть не может.
Приведем пример для k=1:
M11=5
M21=4
Приведем пример для k=2:
Из уравнения
(X1 + X2 +Xn-1 + Xn+1 +Xn+2+Xk) -Xn <=0
для k=2 имеем :
X1-X2<=0
X2-X1<=0
Такое возможно только когда : X1=X2
Пусть , например,
M11=7 ; M12 = 5 ;
M21=6 ; M22= 4
X1=X2=1
7+4 = 6+5 = 11 ( верно)
Пошаговое объяснение:
1.
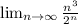
исследуем по признаку Даламбера
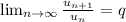
если q < 1, то ряд расходится, если q > 1, то сходится, если =1 неопределенность
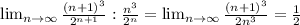
ряд сходится
2.
область сходимости ряда это [-R; R], где
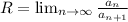
у нас 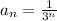
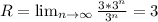
x₁ = 1-3 = -2
x₂ = 1+3 = 4
ряд абсолютно сходится при всех x ∈ (-2;4)
теперь на концах
х = -2
∑ 1/3ⁿ *(-3)ⁿ = (-1)ⁿ
знакочередующийся ряд
по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего.
у нас 1=1=1 - не выполняется.
по второму признаку - предел ряда должен стремиться к нулю (при n стремящейся к бесконечности)
у нас 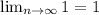
точка х = -2 есть точка расходимости
х = 4
исследуем при интегрального признака сходимости
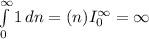
точка х = 4 так же точка расходимости
3.
тут я не совсем уверена. вот что помню из института....
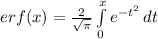
так что, извините, если что не так
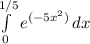
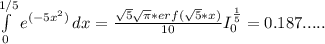
Примем остаток денег после покупки билета на катер за 1, тогда
1) 1-3/8=5/8 - часть денег, оставшаяся после покупки открыток и она равна 35 рублей, значит всего осталось денег:
2) 35*8/5=56 (руб) - осталось после того, как купила билет на катер
3) 336-56=280 (руб.) - стоил билет на катер