Пошаговое объяснение:
Пусть ε - сколь угодно малое положительное число. Мы докажем утверждение, если найдём такое число δ>0, если для всех x∈(3-δ; 3+δ) будет выполняться неравенство /(x²-9)/(x²+3*x)-2/<ε. Это неравенство равносильно двойному неравенству 2-ε<(x²-9)/(x²+3*x)<2+ε. Их общим решением является x∈(3/[1+ε];3)∪(3;3/[1-ε]). Так как число 3/(1+ε) "ближе" к 3, чем число 3/(1-ε), то возьмём δ=3-3/(1+ε)=3*ε/(1+ε). Таким образом, число δ найдено, а это и доказывает справедливость равенства.
ответ: x1=2± x2=1±i
x2=1±i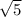 x3=1±
x3=1±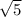 x4=2
x4=2
Пошаговое объяснение:
пусть x^2-3x=y (Чтобы много не писать)
||y|-5|=x+1
|y|-5=x+1 |y|-5=-x-1
|y|=x+6 |y|=4-x
y=x+6 y=-x-6 y=4-x y=x-4
x^2-3x=x+6 x^2-3x=-x-6 x^2-3x=4-x x^2-3x=x-4
x^2-4x-6=0 x^2-2x+6=0 x^2-2x-4=0 x^2-4x+4=0
D=40 D=-20 D=20 D=0
x1=2± x2=1±i
x2=1±i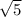 x3=1±
x3=1±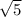 x4=2
x4=2
б) наливаем в необходимую емкость 2 раза по 5-литрововому сосуду, получаем 10 л. Затем в 17-литровый сосуд 3 раза наливаем воду 5- литровым сосудом, а на 4 раз выливая воду в 17 -литровый у нас остается 3 литра воды в 5 литровом сосуде, которые и выливаем к 10 литрам
в)наливаем в 7-литровое ведро 2 раза по 3 л( в ведре получится 6 л), на третий раз переливая из банки в ведро (1 л) у нас в банке остается 2 л.Эти 2 литра переливаем в кастрюлю и добавляем еще одну 3-литровую банку, получаем 3+2=5
г)набрать в 9-литровое ведро 2 раза по 4 литра(получится 8 л), а на 3-ий раз выливая из 4-литровой емкости у на остается в ней 3 литра (4-1=3 литра),которые переливаем в необходимую емкость. И так повторяем еще раз, т.е 3+3 =6л